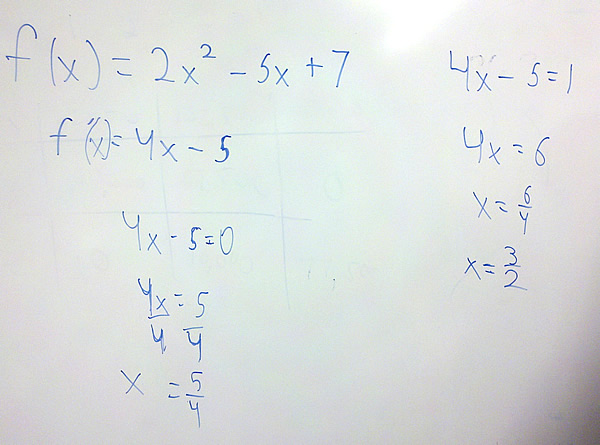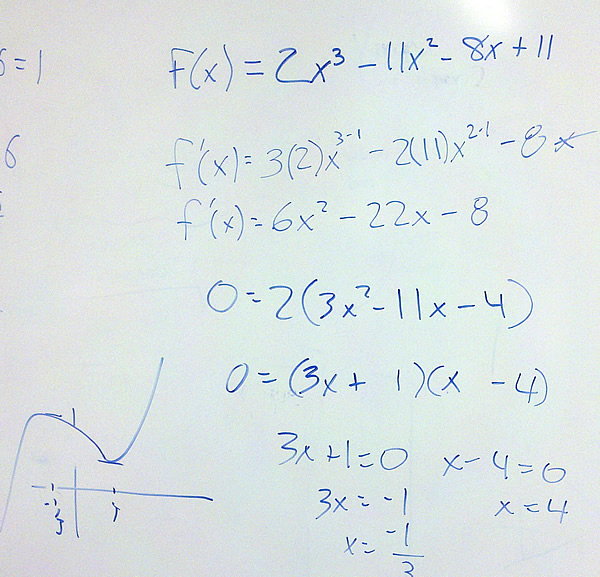A few of you had trouble with the problems referring to slopes of tangent lines. Remember, the slope of a tangent line to a function is given by the derivative. So by setting the derivative equal to the desired slope value, we can solve for the x value.
Problem 1 For the function $latex f(x)=3{{x}^{2}}-4x+1$.
-
- Find where the tangent line is horizontal.
- Find where the tangent line’s slope is equal to -1.
Problem 2 For the function $latex f(x)=2{{x}^{2}}-5x+7$.
-
- Find where the tangent line is horizontal.
- Find where the tangent line’s slope is equal to 1.
Problem 3 For the function $latex f(x)=2{{x}^{3}}-11{{x}^{2}}-8x+1$.
-
- Find where the tangent line is horizontal.
In this last example, you need to factor the quadratic to find the two places where the tangent line is horizontal (has a slope of zero). In some instances, you might need to use the quadratic formula to solve the equation.