Problems that ask you to solve for the rate r in the compound interest formula require the use of roots or creative use of exponents. Let’s look at an example.
Problem Suppose 5000 dollars is deposited in an account that earns compound interest that is done annually. If there is 7000 dollars in the account after 2 years, what is the annual interest rate?
Solution The easiest way to approach this problem is to use the compound interest formula,
This formula applies when interest is earned on an annual basis and the interest is earned once a year.
Let’s look at the quantities in the problem statement:
- 5000 dollars is deposited in an account > P = 5000
- If there is 7000 dollars in the account after 2 years > A = 7000 and n = 2
Putting these values into the formula above gives us
We need to find the annual interest rate r. Since the r is hidden in the parentheses, we start by isolating the parentheses.
To get at the r, we need to remove the square on the parentheses.
Using a calculator to do the square root, we get r ≈ 0.183 or 18.3%.
Although most calculators have a square root key, when removing powers it is often useful to raise both sides to a power. For instance, we could remove the square by raising both sides to the ½ power.
When you raise a power to another power, you multiply the exponents 2 ∙ ½ = 1. The right side simply becomes 1 + r. Now we can solve for r:
Using the power key on your calculator gives the same answer as before. Make sure the 1/2 power is entirely in the power. You can make sure this happens using parentheses: (7000/5000)^(1/2)-1.
Now what if the interest is earned over six years instead of two years? Instead of a square on the parentheses we now have a sixth power.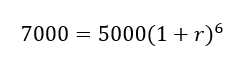
To solve for r in this equation, we follow similar steps.
The root can be computed on a graphing calculator using the MATH button or put into WolframAlpha: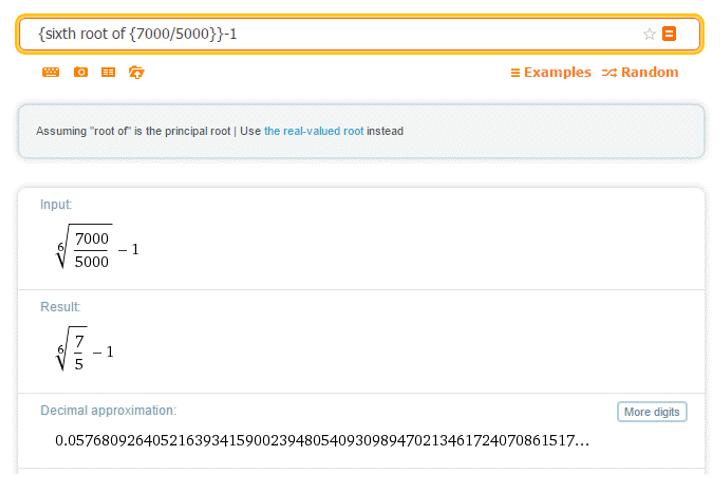
Either method gives r ≈ 0.577 or 5.77%. Notice that the annual interest is lower when it is earned over a longer period of time.
If we use a 1/6 power to solve for r, we would carry out the steps below: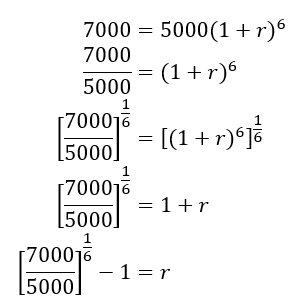
Using a 1/6 power on your calculator gives the same answer as above.


