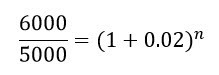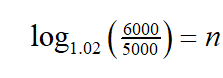Suppose 5000 dollars is deposited in an account that earns 2% compound interest that is done annually. In how many years will there be 6000 dollars in the account.
This problem requires the use of the compound interest formula,
This formula applies when interest is earned on an annual basis and the interest is earned once a year.
Let’s look at the quantities in the problem statement:
- 5000 dollars is deposited in an account > P = 5000
- that earns 2% compound interest that is done annually > r = 0.02
- Will there be 6000 dollars in the account > A = 6000
Putting these values into the formula above gives us
Unlike other problems where we solve for P or r, here we need to solve for the power in the right hand side, n. Solving for a value in the power requires the property of logarithms, log(yx) = x logy. It allows us to move the n in the power and change it to a multiplier. But before we can apply this property, we isolate the factor containing the n:
Now take the logarithm of both sides of the equation:
This gives us
or n ≈ 9.21 years.
Another way we could solve 
is to convert directly to a logarithm,
This can be evaluated using the LOGbase command under the MATH menu on a graphing calculator.
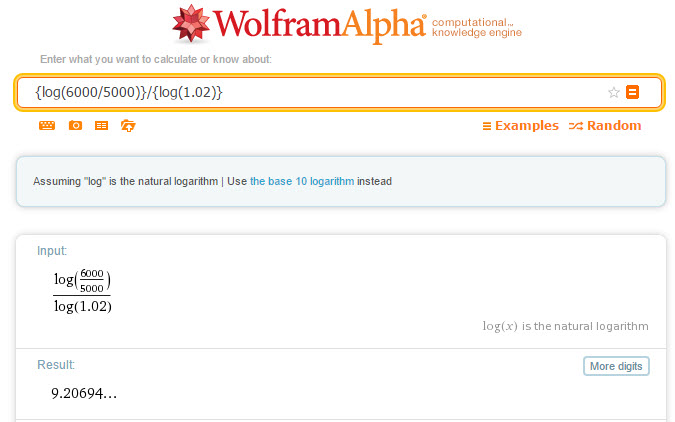
In WolframAlpha, we could evaluate the logs as follows.
or by simply typing into WolframAlpha
