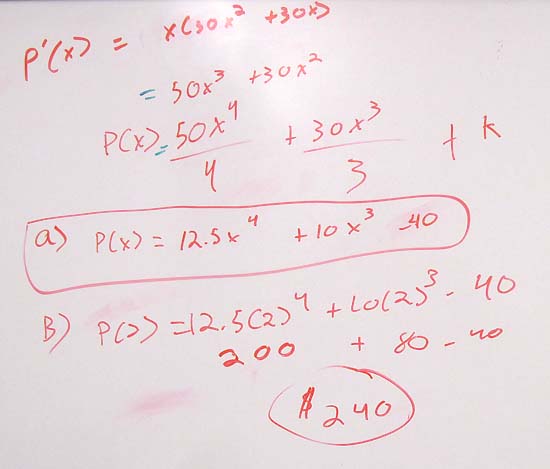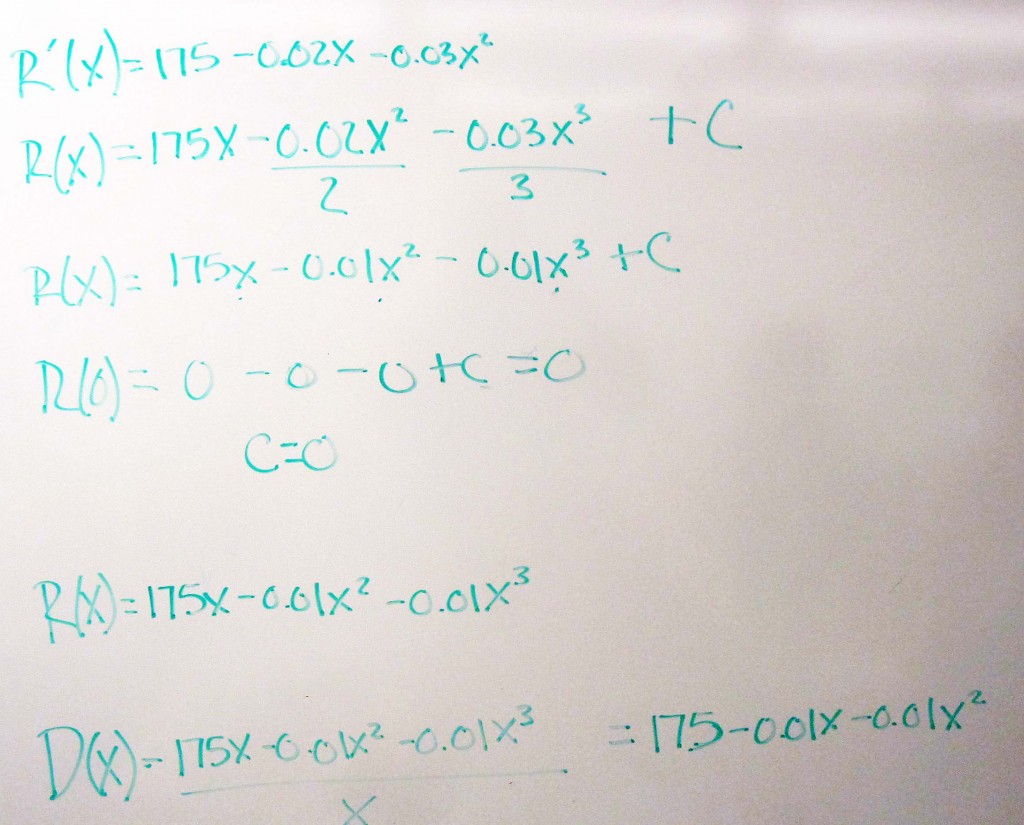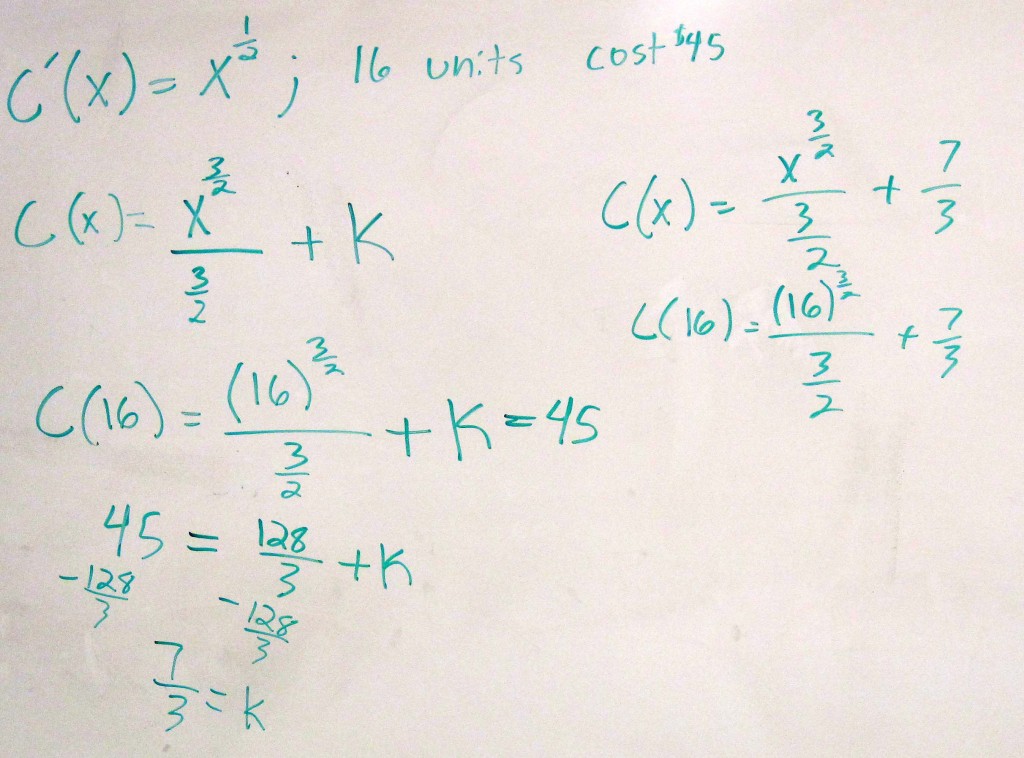Marginal function like marginal cost, marginal revenue, and marginal profit are all derivatives. This means that we can undo these derivatives to obtain the cost, revenue, and profit functions by taking their antiderivatives.
For example, suppose the marginal cost for a product is given by
$latex \displaystyle {C}'(x)=0.2{{x}^{2}}+5x$
where x is the number of units produced. Also suppose the fixed cost are 1000 dollars. The antiderivative of the marginal cost is
$latex \displaystyle C(x)=\frac{0.2}{3}{{x}^{3}}+\frac{5}{2}{{x}^{2}}+K$
where K is an arbitrary constant. By requiring that the fixed cost is 1000 dollars, we know that the cost of producing no items is $1000 or C(0) = 1000. This means that
$latex \displaystyle C(0)=\frac{0.2}{3}\cdot {{0}^{3}}+\frac{5}{2}\cdot {{0}^{2}}+K=1000$
or K = 1000. The cost function matching the marginal cost and fixed cost is
$latex \displaystyle C(x)=\frac{0.2}{3}{{x}^{3}}+\frac{5}{2}{{x}^{2}}+1000$
Here are several more examples worked out by students.
Example 1 Find the demand function corresponding to the marginal revenue
$latex \displaystyle {R}'(x)=175-0.02x-0.03{{x}^{2}}$
Remember, no revenue is incurred when no items are sold.
Example 2 Find the cost function corresponding to the marginal cost function
$latex \displaystyle {C}'(x)={{x}^{\tfrac{1}{2}}}$
Assume that 16 units costs 45 dollars.
Example 3 The marginal profit in dollars per pound on Brie cheese is
$latex \displaystyle {P}'(x)=x\left( 50{{x}^{2}}+30x \right)$
where x is the amount of cheese sold in hundreds of pounds. Assume the profit is -40 when no cheese is sold.
a. Find the profit function.
b. Find the profit from selling 200 pounds of cheese.
Since the variable x is in hundreds of pounds, the profit is found by substituting 2 (not 200) into the function.