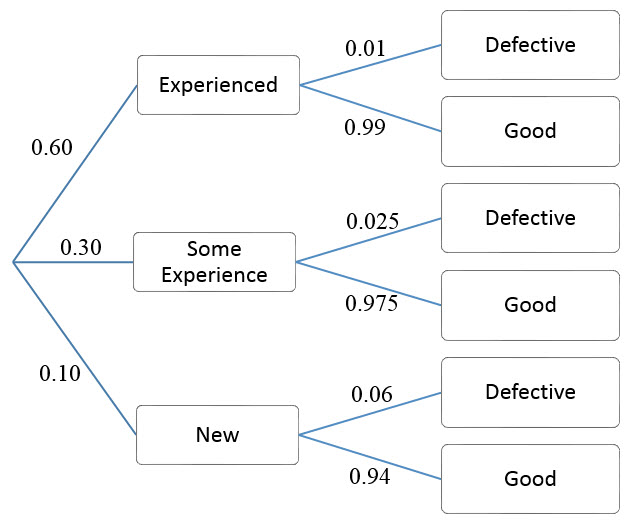
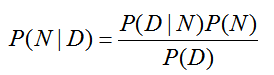Based on past experience, a company knows that an experienced machine operator (one or more years of experience) will produce a defective item 1% of the time. Operators with some experience (up to one year) have a 2.5% defect rate, and new operators have a 6% defect rate. At any one time, the company has 60% experienced operators, 30% with some experience, and 10% new operators. Find the probability that a particular defective item was produced by a new operator.
The first thing we need to do is organize the information we have been given. So let’s create some events to work with.
D: “operator produces a defective item”
E: “experienced operator”
S: “operator with some experience”
N: “new operator”
With these definitions, the information in the problem statement can be written as
P(E) = 0.60 P(D | E) = 0.01
P(S) = 0.30 P(D | S) = 0.025
P(N) = 0.10 P(D | N) = 0.06
The tree diagram below reflects this information.
If we want to know the probability that an experience operator produces a defective item, we are interested in the event E and D. These probabilities lie along the top branch so
To find the probability that a particular defective item was produced by a new operator, we need to compute P(N | D). The appropriate form of Baye’s Theorem is
Solving for P(N | D) yields
Both factors in the numerator are branches in the tree. The denominator is simply the sum of the branches leading to defective or
The key to using Bayes’ Theorem is to write the proper tree and appropriate rule based on the events in the problem.