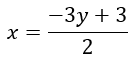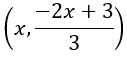Suppose you are solving a system such as
2x + 3y = 3
4x + 6y = 6
Solving this system with substation or elimination leads to 0 = 0. This is a signal that there are an infinite number of solutions. This does not mean that ANY ordered pairs will solve the system. Only certain combinations of x and y will work. You need a way of finding any of those solutions. There are two ways to do this.
Method 1: Start with one of the equations (it does not matter which one) like 2x + 3y = 3. Solve this equation for x: 2x = -3y + 3 and then
If you have a value for y, this gives you a corresponding value for x. For instance, if y = 1, the corresponding x value is x = 0. This gives us one possible solution, (0, 1). If y = -1, then x = 3 giving us (3, -1). In general, we can write all solutions out as
Picking any value for y will give you a corresponding value for x which solves the system.
Method 2: What if we were to take 2x + 3y = 3 and solve for y. In this case we would get . If we were to pick values for x, we get corresponding values for x. For instance, if x = 0 we get y = 1 or the ordered pair (0, 1). Notice that this is one of the same ordered pairs as in Method 1. Let’s try another value for x, x = 3. When we put this into
![]()
Both ways of writing the solution give the same ordered pairs. In Method 1, you pick a value for y and find the corresponding x value. In Method 2, you pick a value for x and find the corresponding y value. Since the values you pick can be anything, this gives the infinite number of ordered pairs that solve the system.