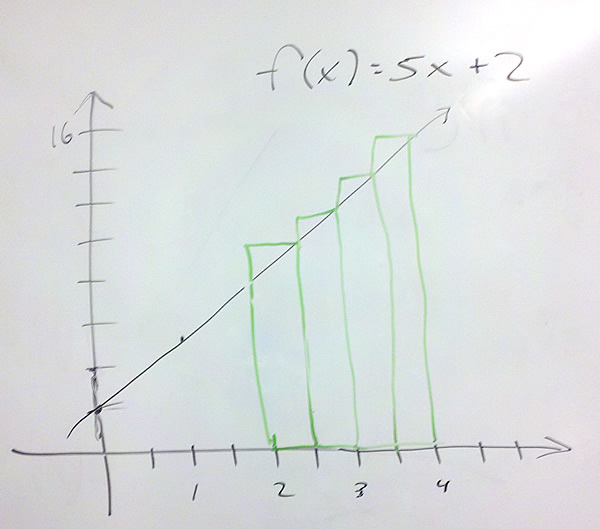
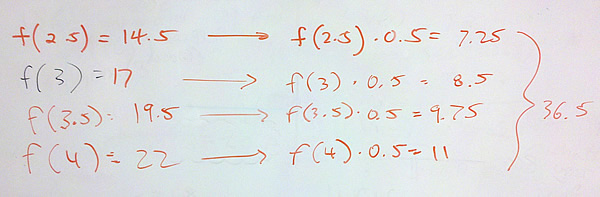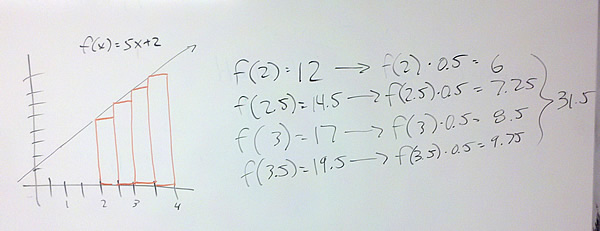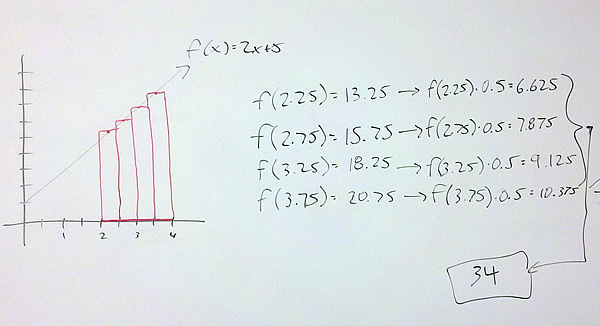Problem 1 Approximate the area under $latex \displaystyle f(x)=5x+2$ with 4 rectangles using a) right hand rectangles, b) left hand rectangles, and c) midpoint rectangles.
a) Right hand rectangles
b) Left hand rectangles
c) Midpoint Rectangles
Notice that each of these parts does essentially the same thing…multiply an f(x) value for the height of a rectangle by a width. Notationally, we can write this as
$latex \displaystyle f({{x}_{i}})\cdot \Delta x$
where $latex \displaystyle {{x}_{i}}$ is the x value where the rectangle touches the curve and $latex \displaystyle \Delta x$ is the width of the rectangle. So we can use summation notation for the sum,
$latex \displaystyle \sum\limits_{i=1}^{n}{f({{x}_{i}})\cdot \Delta x}$
where there are n rectangles. The sigma indicates that we are adding up terms with a particular format…in this case, function values time a width.