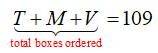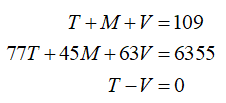More Systems of Linear Equations: Delivering Yarn in Canada

Often the most difficult part of solving a system of equations problem is writing out the system from a word description. In this FAQ, we look at a complicated sounding problem and form a system of linear equations from the problem.

Basket of yarn — A basket of yarn, from http://www.pixelverve.com/raen/2004/07/mini-stash-addition.html {{cc-by-sa-2.0}}

Let’s look at the problem below.

A knitting shop orders yarn from three suppliers in Toronto, Montreal, and Victoria. One month the shop ordered a total of 109 boxes of yarn from these suppliers. The delivery costs were 77 dollars. 45 dollars. and 63 dollars per box for the orders from Toronto, Montreal, and Victoria respectively, with total delivery costs of 6355 dollars. The shop ordered the same amount from Toronto and Victoria. How many boxes were ordered from each supplier?

When beginning a problem involving systems of equations, we need to define the variables in the problem. In this problem, we are looking for the number of boxes ordered from each location. With this in mind, we define

T: number of boxes ordered from Toronto
M: number of boxes ordered from Montreal
V: number of boxes ordered from Victoria

There are several pieces of information we can use to write out equations. The information “the shop ordered a total of 109 boxes of yarn from these suppliers” gives us

This information is distinguished by the fact that it is a total involving the variables.

semi truck making deliveries — Bedwards2044 [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)], from Wikimedia Commons

Let’s look for another piece of information involving a total. The problem also gives the total delivery costs, 6355 dollars. We can use this to write out another equation if we can write out the delivery costs to each supplier. If a single box costs 77 dollars to deliver to Toronto, T boxes will cost 77T dollars to deliver to Toronto. Following this pattern, we write out

77T: cost to deliver T boxes to Toronto
45M: cost to deliver M boxes to Montreal
63V: cost to deliver V boxes to Victoria

This means to shipping costs to each city is related to the total costs by

The final equation may be written using the information, “The shop ordered the same amount from Toronto and Victoria”. This tells us that

If we put all of these equations together, we get the system of linear equations,

Move the variables to the left side of the equation to prepare the system for solving. This gives the system,