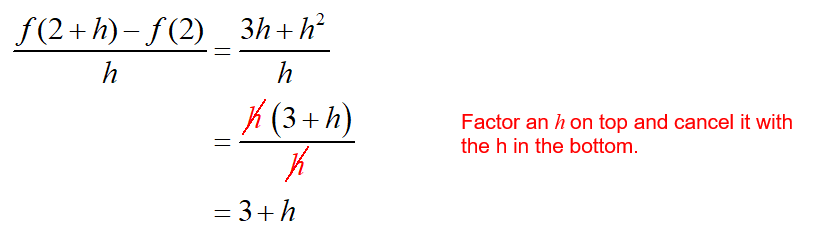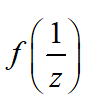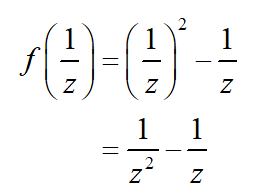The example below demonstrates some ways that function notation can be used.
For the function f (x) = x2 – x, answer each of the questions.
a. Find the value of f (2) .
Solution To find f (2), we need to replace the x in the formula with 2,
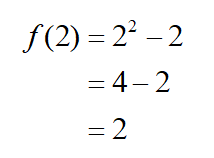
b. Find 
Solution Although the input is not a number, we still evaluate the function by replacing the x with the input. In this case, we replace x with 1/z :
c. Find all values of x for which f (x) = 6.
Solution Instead of supplying the input to the function, the output is supplied instead. To solve this part, set the formula equal to 6 and solve for x.
We can check that these values are correct by putting them into the function:
d. Find f (2 + h).
Solution Replace x with 2 + h in the function,
The output has been simplified by noting that (2 + h)2 is multiplied by FOILing:
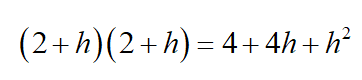
e. The expression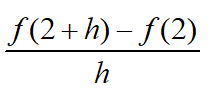 
is called a difference quotient. Find the value of this difference quotient.
Solution In part a we found that f (2) = 2 and in part d we found that f (2 + h) = 2 + 3h +h2.
This means that
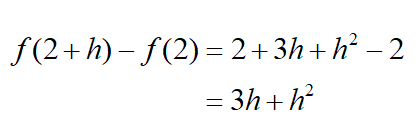
To complete the difference quotient, divide this expression by h:
