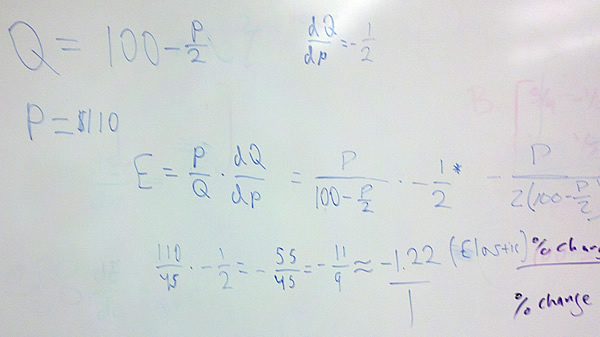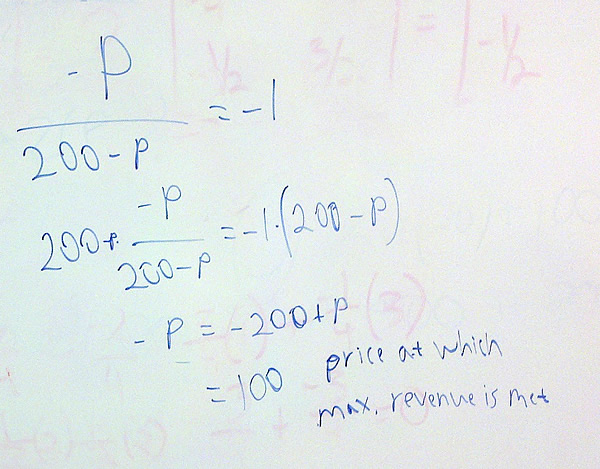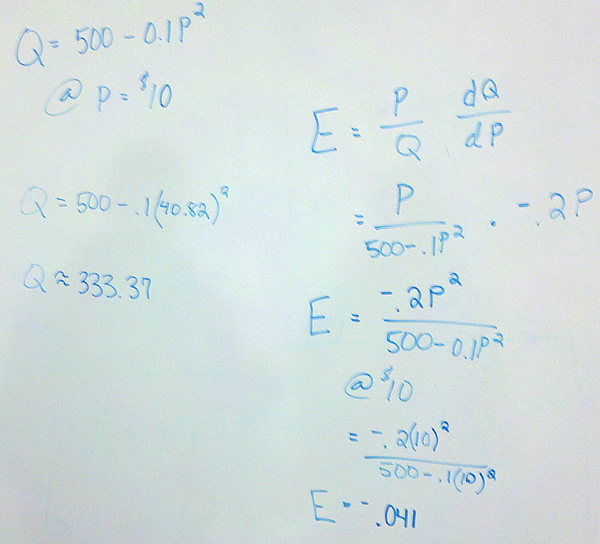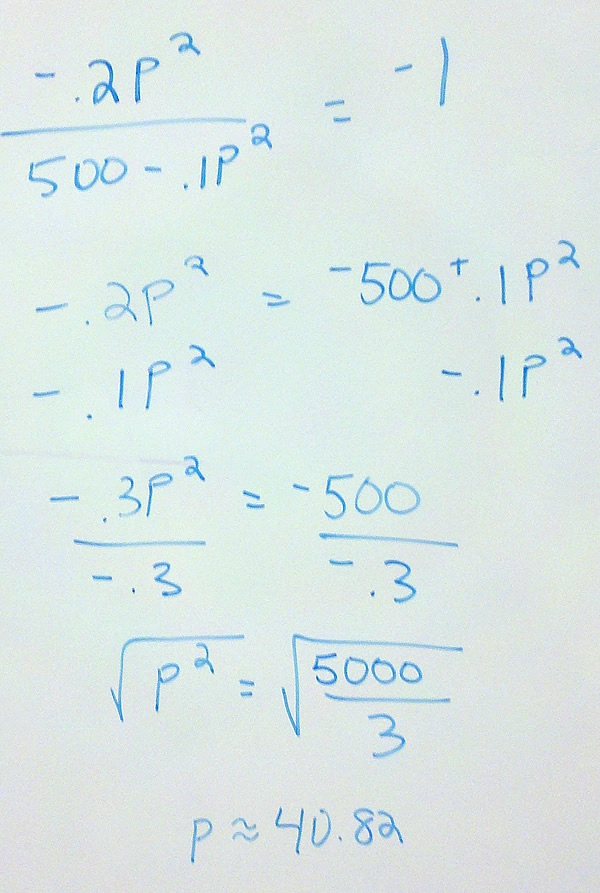Here are several problems classes have worked out to calculate the elasticity E,
$latex \displaystyle E=\frac{P}{Q} \frac{dQ}{dP}$
In this formula, $latex \displaystyle \frac{dQ}{dP}$ is the derivative of the demand function when it is given as a function of P. Here are two examples the class worked.
Problem 1 Suppose the quantity demanded by consumers in units is given by $latex Q=5000-5P$ where P is the unit price in dollars.
-
- Find the elasticity of demand with respect to price when P = 200.
- Find the quantity at which revenue is maximized.
This means that a 1% increase in price results in a 0.25% drop in the quantity demanded. The demand is inelastic and the price increase results in an increase in revenue.
Problem 2 Suppose the quantity demanded by consumers in units is given by $latex Q=100-\frac{P}{2}$ where P is the unit price in dollars.
-
- Find the elasticity of demand with respect to price when P = 110.
- Find the quantity at which revenue is maximized.
This means that a price increase of 1% will lead to a 1.22% drop in demand, demand is elastic and the price increase results in a drop in revenue.
Problem 3 Suppose the quantity demanded by consumers in units is given by $latex Q=500-0.1{{P}^{2}}$ where P is the unit price in dollars.
-
- Find the elasticity of demand with respect to price when P = 100.
- Find the quantity at which revenue is maximized.
An increase of 1% in price results in a drop in demand of 0.041%…demand is inelastic so the increase will result in an increase in revenue.