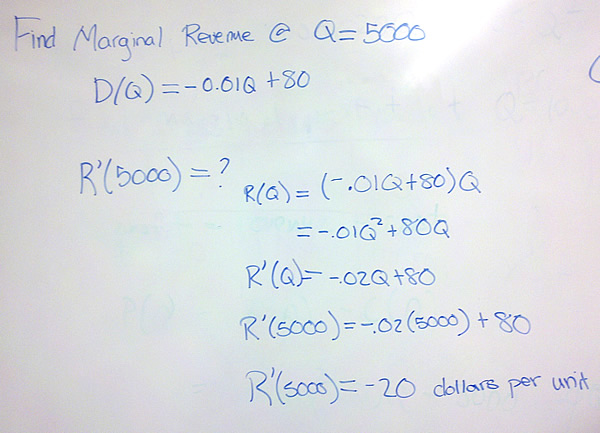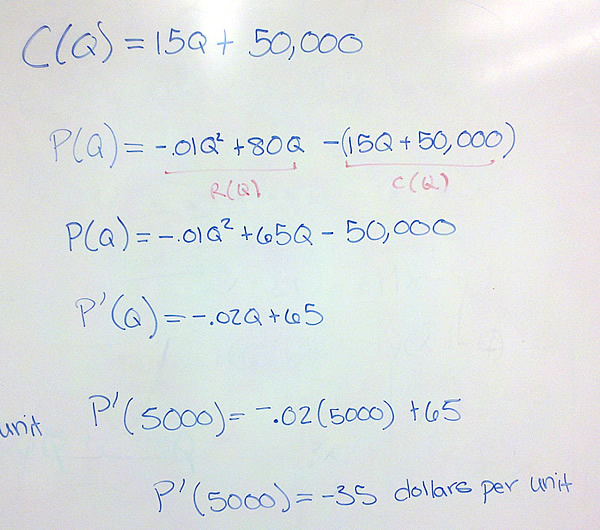What is Marginal Analysis?

Marginal analysis can be daunting because the problems have a few steps. But there are a few basic relationships you can use.

Revenue = Price * Quantity

Profit = Revenue – Cost

 To estimate any marginal function, take its derivative. Here are a few examples from class.

Problem 1 Suppose the demand function is given by  D(Q) = -0.05Q + 100 dollars per unit where Q is the number of units demanded by consumers.

1. 1. Find and interpret the marginal revenue at Q = 700 units.
   2. If the cost function is given by C(Q) = 9Q + 5650 dollars, find and interpret the marginal profit at Q = 700.

This tells us that the 701st unit increases the revenue by 30 dollars.

The 701st unit increases profit by 21 dollars.

Problem 2 Suppose the demand function is given by D(Q) = -0.01Q + 80 dollars per unit where Q is the number of units demanded by consumers.

1. 1. Find and interpret the marginal revenue at Q = 5000 units.
   2. If the cost function is given by C(Q) = 15Q = 50000 dollars, find and interpret the marginal profit at Q = 5000.

The 5001st unit decreases revenue by 20 dollars.

The 5001st units decreases profit by 35 dollars.