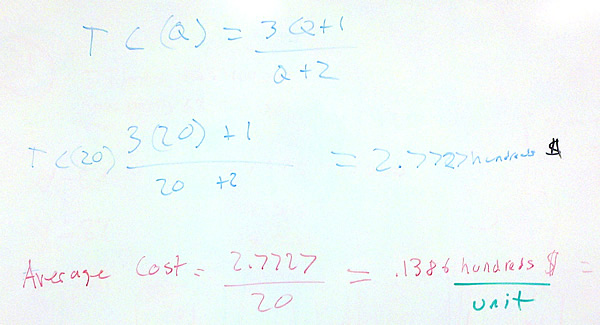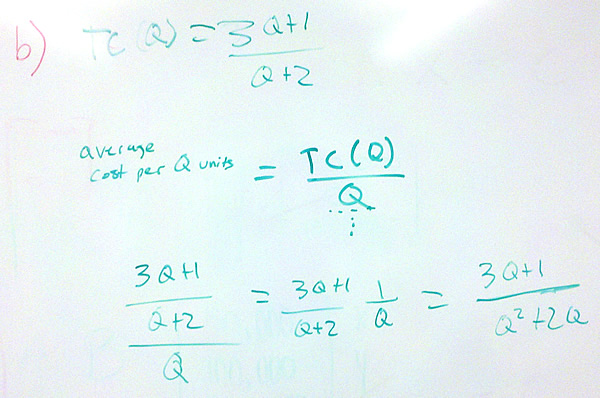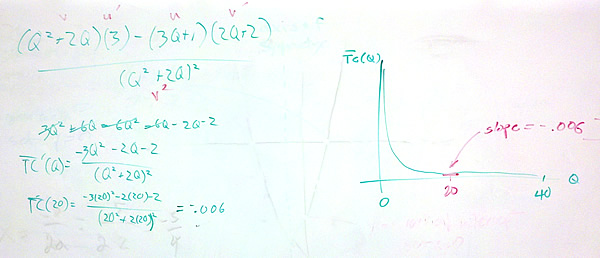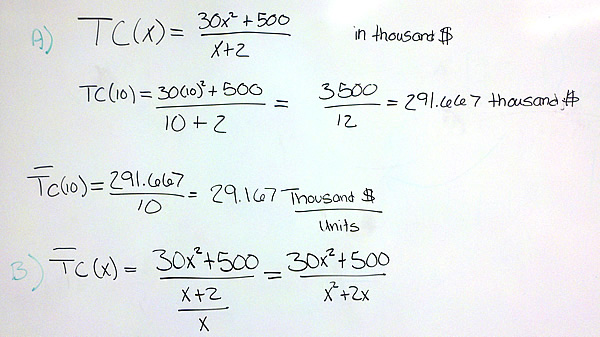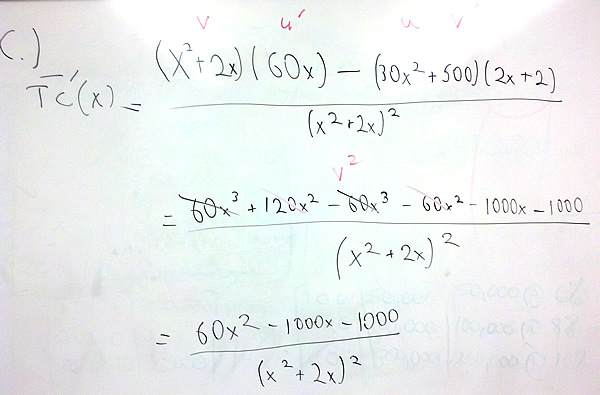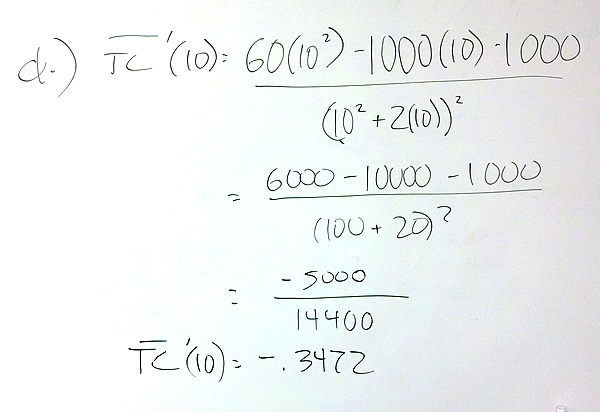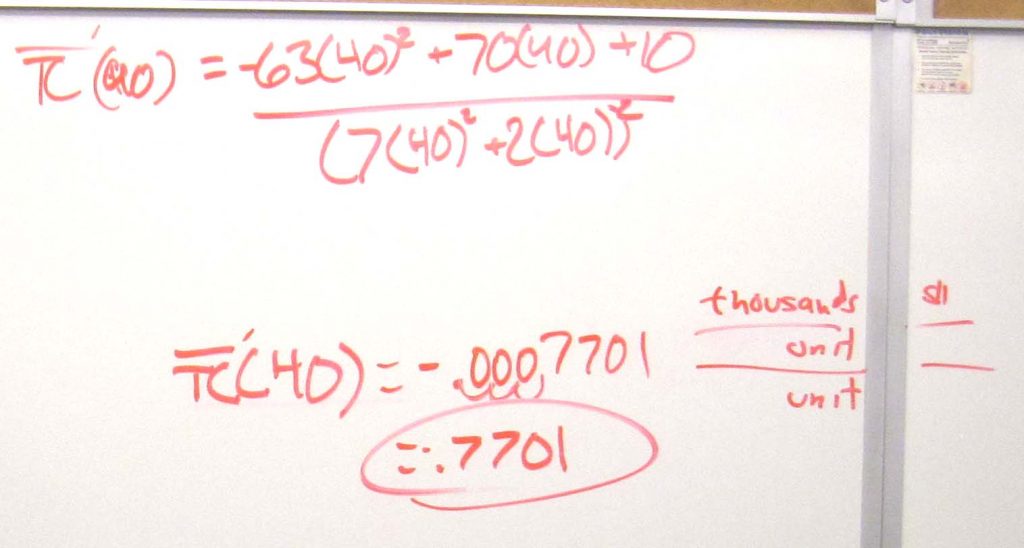In each problem below, the average cost function by dividing the cost function by the variable representing the quantity. For a cost function C(Q), the average cost function is
$latex \displaystyle \overline{C}(Q)=\frac{C(Q)}{Q}$
The marginal average cost function is the derivative of the average cost function.
Problem 1 Suppose the total cost function for a product is
$latex \displaystyle TC(Q)=\frac{3Q+1}{Q+2}\text{ hundred dollars}$
where Q is the number of units produced.
-
- Find the average cost of producing 20 units.
- Find the average cost function.
- Find the marginal average cost function.
- Find and interpret the marginal average cost when 20 units are produced.
This means that each of the 20 units costs an average of .1386 hundred dollars or $13.86.
In this board they have used the fact that dividing by Q is the same as multiplying by 1/Q.
Although it is OK to leave the derivative unsimplified, they need to put in 20. So it is best to do some algebra before putting in the value. Since -0.006 is the slope of the tangent line on the average cost function, the units on it is hundreds of dollars per unit per unit:
$latex \displaystyle \frac{-0.006}{1}\frac{\frac{\text{hundreds of dollars}}{\text{unit}}}{\text{unit}}$
This means that if production is increased by 1 unit, the average cost will drop by 0.006 hundred dollars per unit.
Problem 2 Suppose the total cost function for a product is
$latex \displaystyle C(x)=\frac{30x^{2}+500}{x+2}\text{ thousand dollars}$
where x is the number of units produced.
-
- Find the average cost of producing 10 units.
- Find the average cost function.
- Find the marginal average cost function.
- Find and interpret the marginal average cost when 10 units are produced.
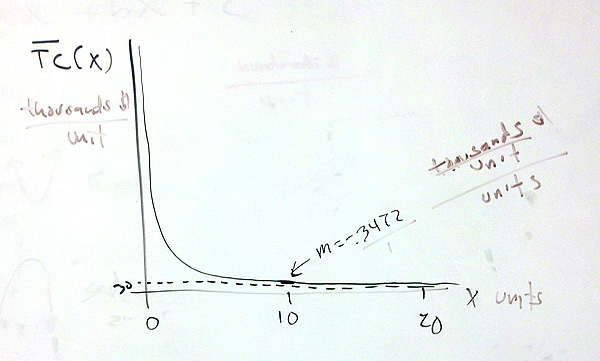
This value tells us that if production is increased by 1 unit, the average cost will drop by 0.3472 thousand dollars per unit or $347.2 per unit. Had they rounded one more decimal place, we would have had this number to the nearest penny.
Problem 3 Suppose the total cost (in thousands of dollars) to produce Q units is
$latex \displaystyle TC\left( Q \right)=\frac{9Q-5}{7Q+2}$
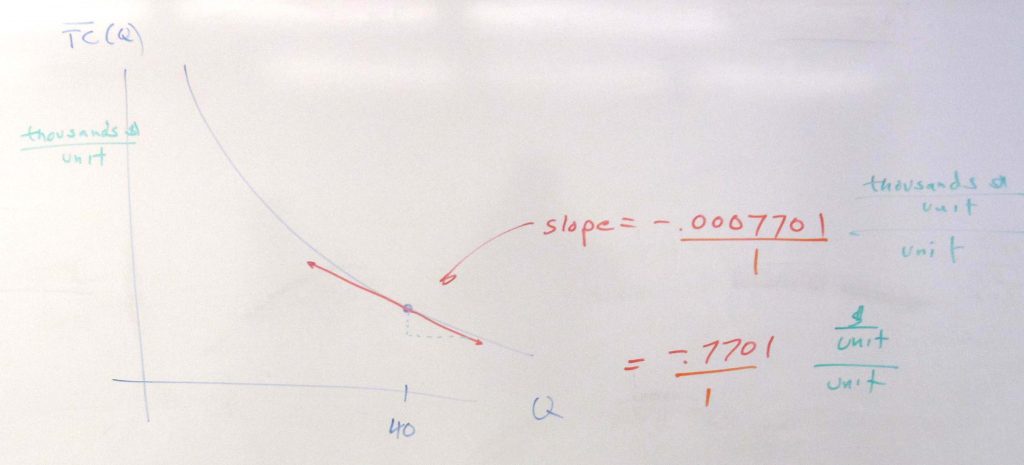
a. Find the the average cost of producing 40 units.
b. Find the average cost function $latex \displaystyle \overline{TC}\left( Q \right)$.
c. Find the marginal average cost function $latex \displaystyle \overline{TC}{{\,}^{\prime }}\left( Q \right)$.
d. Find and interpret $latex \displaystyle \overline{TC}{{\,}^{\prime }}\left( 40 \right)$.
The marginal average cost is simply the slope of the tangent line to the average cost$latex \displaystyle \overline{TC}{{\,}^{\prime }}\left( Q \right)$. The slope has vertical units of thousands of dollars per unit and horizontal units of units. So the rate has units of thousands of dollars per unit per unit. This means that if the production were to increase by one, the average cost would drop by 0.0007701 thousand dollars per unit or 0.7701 dollars per unit. This means that the average cost is decreasing…probably a good thing for the bottom line.