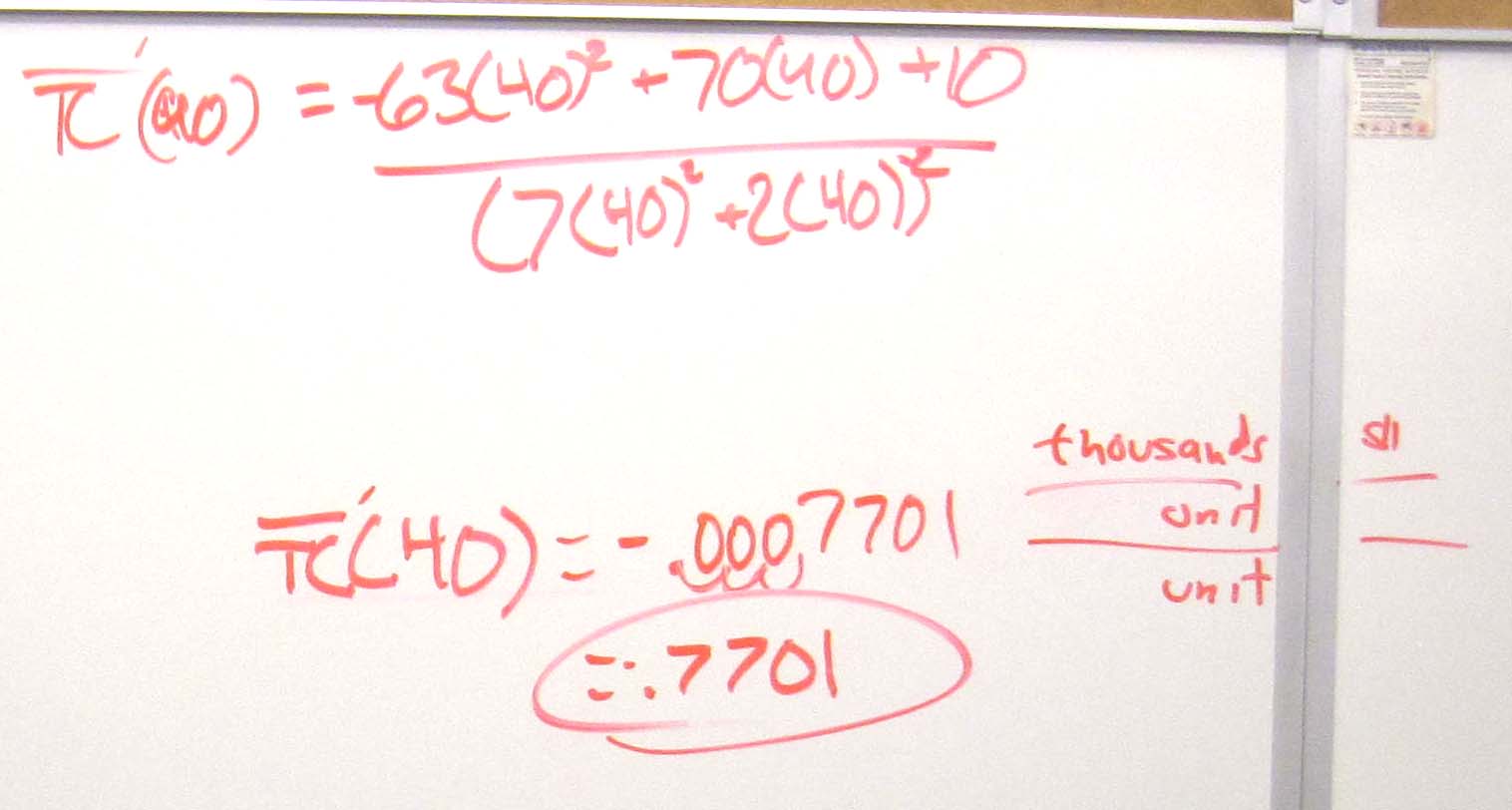To calculate the marginal average cost, we need to first calculate the average cost,
$latex \displaystyle \overline{TC}\left( Q \right)=\frac{TC\left( Q \right)}{Q}$
where TC(Q) is the total cost to produce Q units. Once we have the the average cost function, the marginal average cost is simply its derivative,
$latex \displaystyle \text{Marginal Average Cost}=\overline{TC}{{\,}^{\prime }}\left( Q \right)$
Example Suppose the total cost (in thousands of dollars) to produce Q units is
$latex \displaystyle TC\left( Q \right)=\frac{9Q-5}{7Q+2}$
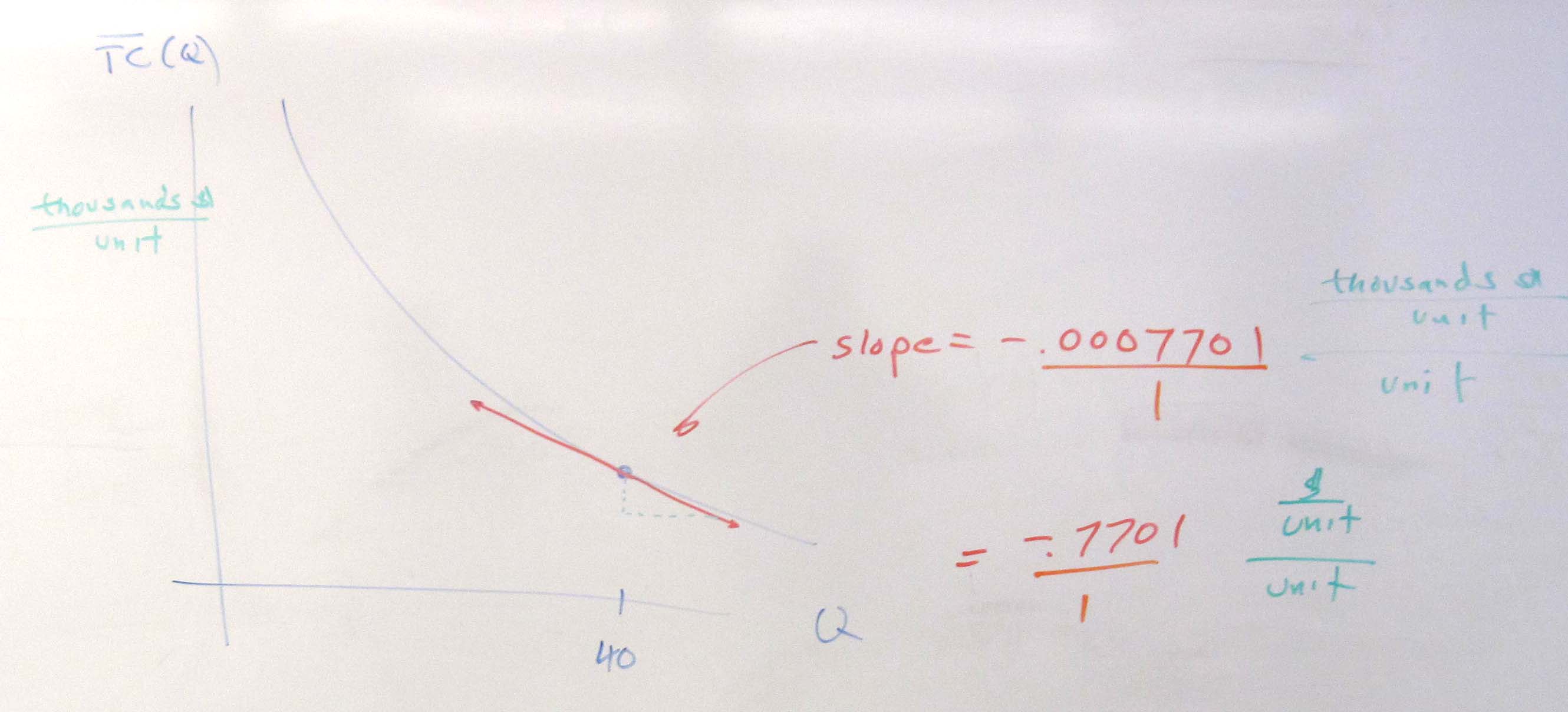
a. Find the the average cost of producing 40 units.
b. Find the average cost function $latex \displaystyle \overline{TC}\left( Q \right)$.
c. Find the marginal average cost function $latex \displaystyle \overline{TC}{{\,}^{\prime }}\left( Q \right)$.
d. Find and interpret $latex \displaystyle \overline{TC}{{\,}^{\prime }}\left( 40 \right)$.