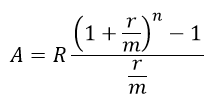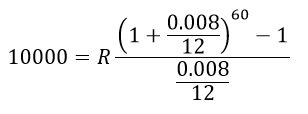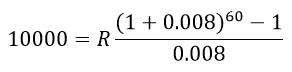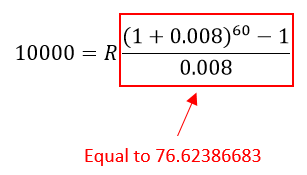What is the difference between these two problems?
Problem A Kanye wants to save $10,000 in 5 years by making monthly payments into an ordinary annuity for a down payment on a condominium at the shore. If the annuity pays 0.80% annual interest compounded monthly, what will his monthly payment be?
VS.
Problem B Kanye wants to save $10,000 in 5 years by making monthly payments into an ordinary annuity for a down payment on a condominium at the shore. If the annuity pays 0.80% monthly interest compounded monthly, what will his monthly payment be?
The key is to notice that the interest rate can be given as an annual rate or a monthly rate. How do we apply the annuity formula,
In this formula,
A: future value
R: payment
m: number of times interest is compounded in a year
r: annual interest rate
n: number of compounding periods
To help us see the difference, think of r/m as the interest rate per period. In Problem A, the annual interest rate is 0.80% and interest is compounded 12 times a year. To solve this problem, we set r = 0.008 and m = 12 and put the other numbers in:
The fraction on the right is equal to 61.19535446.
Solving for R in this equation gives R ≈ 163.41.
In Problem B, the interest rate given to you is the interest rate per period. In other words, r/m = 0.008 This means that in this problem, you need to solve for R in
In this case, the fraction is equal to 76.62386683:
Dividing this number into 10,000 gives a payment of R ≈ 130.51.