What Is The Difference Between A Relative Extrema and An Absolute Extrema?

Relative extrema are simply the bumps and dips on a function’s graph. These are located by tracking where the function changes from increasing to decreasing (relative maximum) or decreasing to increasing (relative minimum). Below are two examples to help you distinguish these types of extrema. The same processes may be used to find the high and low points of functions from applications. This topic is covered in Section 12.1.

Problem 1 Find all relative extrema of

$latex \displaystyle f(x)=2{{x}^{3}}-3{{x}^{2}}-36x$

Solution To find the relative extrema, we must track whether the derivative is zero, positive or negative.

First, let’s find the critical points. Critical point are where the derivative is equal to zero or undefined. The derivative is

$latex \displaystyle {f}'(x)=6{{x}^{2}}-6x-36$

Set the derivative equal to zero. The resulting equation may be solved by factoring.

$latex \displaystyle 6{{x}^{2}}-6x-36=0$

The least common multiple may be factored from the left side,

$latex \displaystyle 6({{x}^{2}}-x-6)=0$

Now factor the trinomial,

$latex \displaystyle 6(x-3)(x+2)=0$

Set each of the factors containing variables equal to zero to give

$latex \displaystyle x=3\quad x=-2$

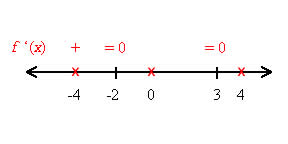
Place these critical numbers along with points on either side of them on a number line.

The critical numbers are labeled with black tic marks on the number line and also = 0 to indicate that they were found by setting the derivative equal to zero. The testing points at -4, 0, and 4 are labeled with an x on the number line. To do the testing, it is useful to have the factored form of the derivative,

$latex \displaystyle {f}'(x)=6(x-3)(x+2)$

Let’s test the derivative at -4. We don’t need the exact value of the derivative…only whether its sign is positive or negative.

$latex \displaystyle {f}'(4)=6(-4-3)(-4+2)$

The factors are +, -, and -. The product is (+)(-)(-) or +. Label a + above -4 to indicate that the derivative is positive.

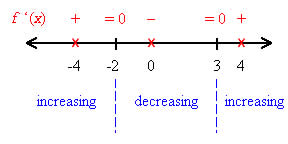
Continue testing at 0 and 4 to fill out the number line below. DON’T assume the signs will alternate. For some functions, this does not happen. The function is increasing where the derivative is positive and decreasing where the derivative is negative. This number line may be used to track the intervals where the function is increasing or decreasing. We can also use it to identify the relative extrema. At x = -2, the function changes from increasing to decreasing so it is a relative maximum. The value of the maximum is

$latex \displaystyle f(-2)=2{{(-2)}^{3}}-3{{(-2)}^{2}}-36(-2)=44$

or (-2, 44).

At x = 3, the function changes from decreasing to increasing so it is a relative minimum. The value of the minimum is

$latex \displaystyle f(-2)=2{{(3)}^{3}}-3{{(3)}^{2}}-36(3)=-81$

or (3, -81).

Absolute extrema are the very highest and lowest points on a graph. If a graph is continuous, we can find the absolute extrema on a closed interval by finding the function values at the critical points and the endpoints.

Problem 2 Find all absolute extrema of