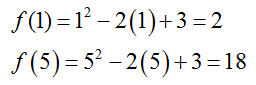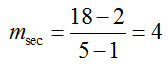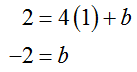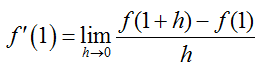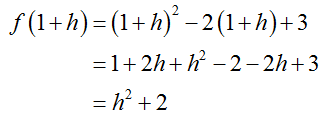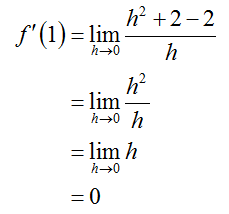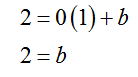Many students struggle with slopes of tangent lines versus slopes of secant lines. In the example below, I find these slopes and use them to compute the equation of a tangent line and the equation of a secant line.
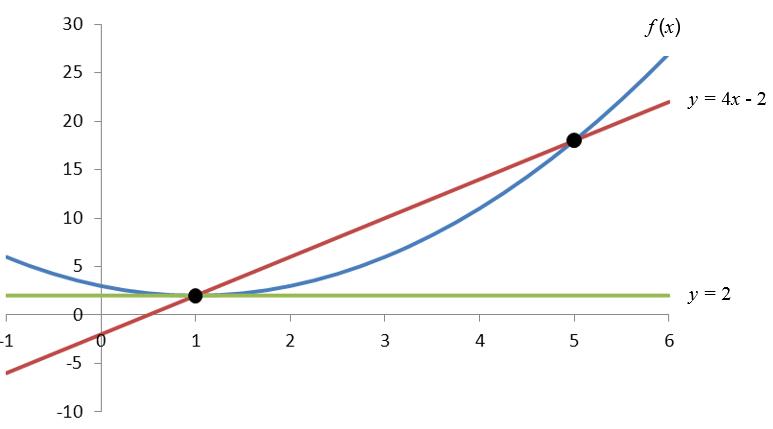
The secant line is the red line to the right that passes through two points on the curve. The tangent line is the green line that just grazes the curve at a point.
For the function f (x) = x2 – 2x + 3, answer each of the questions below.
a. Find the equation of the secant line passing through x = 1 and x = 5.
b. Find the equation of the tangent line at x = 1.
Solution For each of these parts, we’ll find the equation of a line using y = mx + b. For part a, we’ll find the slope of the line using two points on the function. For part b, we’ll find the slope of the line using the derivative of f (x) at x = 1 or f ′(1).
For part a, the line must pass through the point (1, 2) and (5,18) since
The slope of the line is
This gives us the secant line equation y = 4x + b. To find the value of b, substitute one of the points for x and y:
The equation of the secant line is y = 4x – 2.
For part b, the tangent line must pass through (1, 2) with a slope given by f ′(1). The derivative is found by applying the definition of the derivative at a point,
We have already found that f (1) = 2 and the other function value is
The definition of the derivative gives
The equation of the tangent line is y = 0x + b. Substitute (1, 2) to give
The equation of the tangent line is y = 2.
The lines and function are graphed below.
The red line on the graph is the secant line. It passes through (1, 2) and (5, 18) with a slope of 4. The green line is a a tangent line that passes through (1, 2). It is the line that looks most like the function f (x) near x = 1.