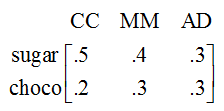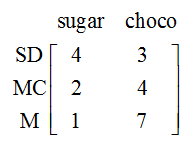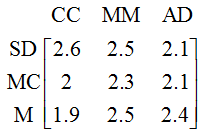With a little practice, it is not too difficult to multiply two matrices. Add WolframAlpha or a graphing calculator to the mix…and you should blaze through the simplest problems. But what good is matrix multiplication?
Each kilogram of Cheery Cherry requires .5 kg of sugar and .2 kg of chocolate, each kilogram of Mucho Mocha requires .4 kg of sugar and .3 kg of chocolate; and each kilogram of Almond Delight requires .3 kg of sugar and .3 kg of chocolate. The cost of 1 kg of sugar is 4 dollars in San Diego, 2 dollars in Mexico City, and 1 dollars in Managua. The cost of 1 kg of chocolate is 3 dollars in San Diego, 5 dollars in Mexico City, and 7 dollars in Managua.Put the information above in a matrix in such a way that when you multiply the matrices, you get a matrix representing the ingredient cost of producing each type of candy in each city.
Start by putting the information in a matrix. There are two ingredients and three types of candy so we need either a 2 x 3 or 3 x 2. Either will be fine as long as we label the rows and columns. I choose to use a 2 x 3:
Because the product has to correspond to candy type and cities, the product must be a 3 x 3 matrix. To get this from the 2 x 3 above, we’ll need to multiply a 3 x 2 times the 2 x 3. Based on the information above, the rows must correspond to cities and the columns to ingredients:
Now let’s carry out the multiplication:
To get the entry in the second row, first column of the product we need to multiply the second row in the first matrix by the first column in the second matrix and add the results:
Other entries are calculated similarly. Since we are multiplying amounts of ingredients times cost per amount, the product is a total cost. How should we label the product?
Using these labels we can locate the cost of any of the three candies in each of the three cities. For instance, the cost of Cheery Cherry is Mexico City would be 2 dollars.