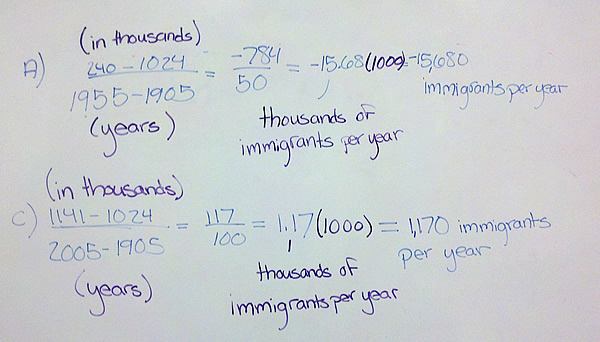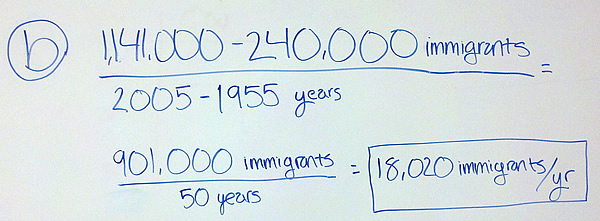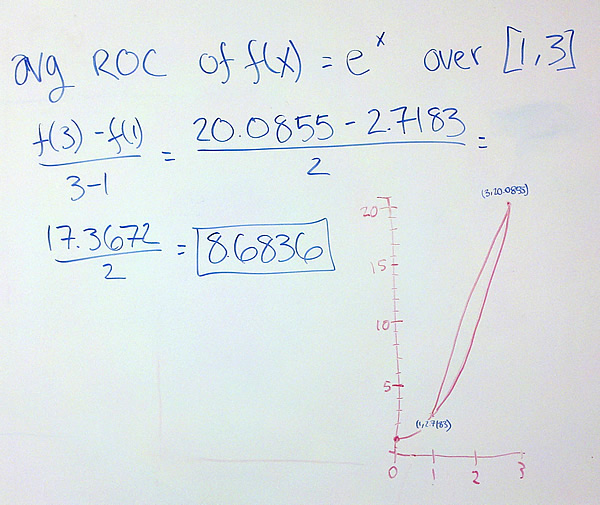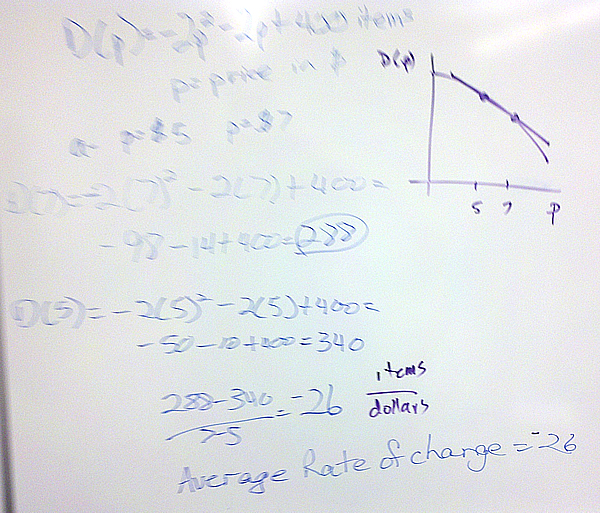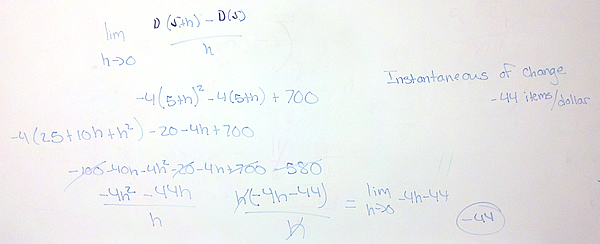We are now in the real meat of calculus….rates and derivatives. Essentially, rates are simply slopes. Depending on the field you are working in or the representation of the data or function, it might have a different terminology. Keeping all of these straight is the biggest challenge in the class. Let’s try to put what we know into a table.
| Common Description | Graphical Interpretation | Mathematical Terminology |
|---|---|---|
| Average Rate of Change of f(x) from x=a to x=b | Slope between (a,f(a)) and (b,f(b)) | Slope of the Secant Line from x=a to x=b |
| Instantaneous Rate of Change of f(x) at x=a | Slope between (a,f(a)) and (a+h,f(a+h)) where h is very small | Slope of the Tangent Line on f(x) at x=a |
If it feels like we use slope to calculate everything…you are right. The only difference is where the two points are located. If they are located fairly far apart, then we are calculating an average rate of change. If they are located an infinitesimal amount apart, then we are calculating the instantaneous rate of change.
But here is where it gets hazy…if the representation of the function does not allow us to pick the points infinitely close together, we may approximate the instantaneous rate of change with an average rate of change between two points that are as close as the representation allows. I think this point is bothering many of you. It occurs most often when we try to find the instantaneous rate from a data table. In that case, the points are where they are at and we can pick pairs that are closer and closer together. We pick them as close as we can near the place we want the instantaneous rate of change and say we are estimating the instantaneous rate of change.
If we are given a graph, we can draw a secant line between the points to calculate the average rate of change. The only estimating done in this case is estimating where the points are on the graph. Our eyes are only so good in reading off the values. For the instantaneous rate of change, we draw the tangent line where we want the rate and eyeball its slope. Again, since we are making educated guesses about the slopes, the numbers are estimates based on our ability to read the slope.
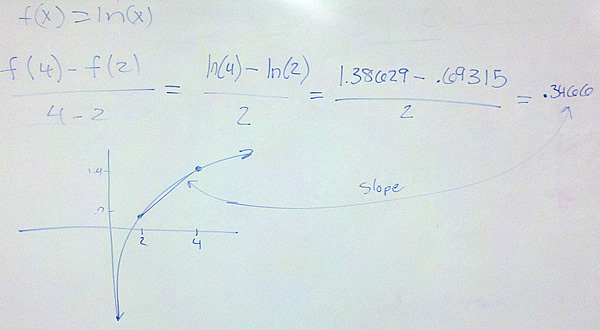
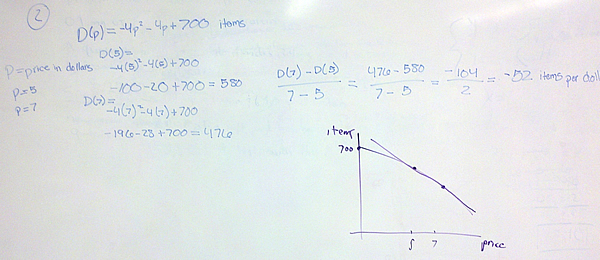
If we are given the function’s formula, we can calculate the average rate or the instantaneous rate exactly. For the average rate of change of f(x) over x = a to x = b, we calculate [latex]{{f(b) – f(a)} \over {b – a}}[/latex].
For the instantaneous rate of change, we use the function’s formula to calculate the limit [latex]\mathop {lim }\limits_{h \to 0} {{f(a + h) – f(a)} \over h}[/latex].
The estimating comes from the fact that we may not be able to find two points infinitesimally close or the fact that we cannot calculate the slope perfectly from how the function is given to us.
Another cautionary note…different disciplines call the derivative by different names. Mathematicians call it the derivative of course, but in physics it might be called the instantaneous rate. In finance and economics, it will be called the marginal function. And in other fields you’ll here other terms.