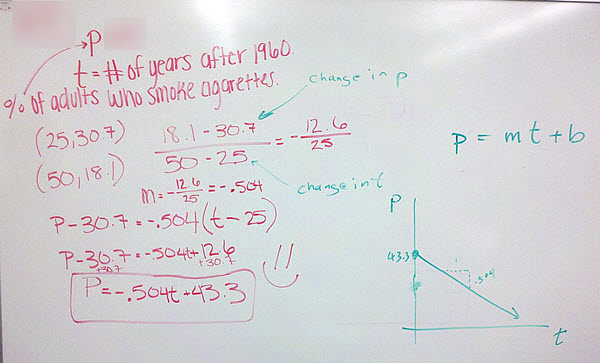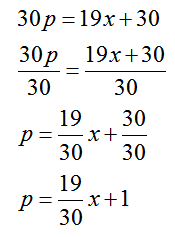In many linear application problems, you needed to write the given information as ordered pairs and then find the equation that passes through the ordered pairs. Here is a similar example that use p = mt + b instead of y = mx + b.
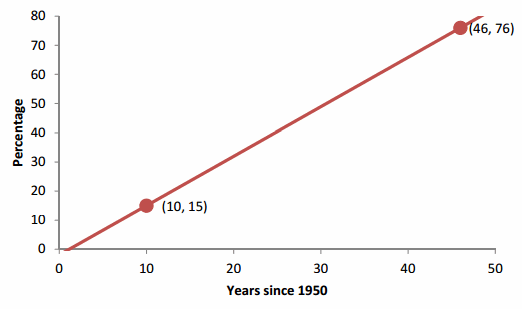
Problem The percent of births to teenage mothers that are out of wedlock can be approximated by a linear function. In 1960, the percentage was 15% and in 1996 the percentage was 76%.
Use this information to find a linear model for the percentage of births as a linear function of the number of years since 1950.
Solution Since the problem statement specifies a linear function of the number of years since 1950, the input to this function is years since 1950 and the output is the percentage. The information in the problem can be written as ordered pairs (10, 15) and (46, 76).
Define the variables for these quantities as
t: years since 1950
p: percentage of births to teenage mothers out of wedlock
This means the form of the linear function is p = mt + b. The slope of a line passing through these points is
The slope is written as a fraction so no rounding occurs. Writing this as a decimal and rounding the amount would lead to a line that does not pass through the points. With this slope, we know the equation of the line is . To find the value of b, substitute one of the ordered pairs into the equation and solve for b.
This makes the linear function,

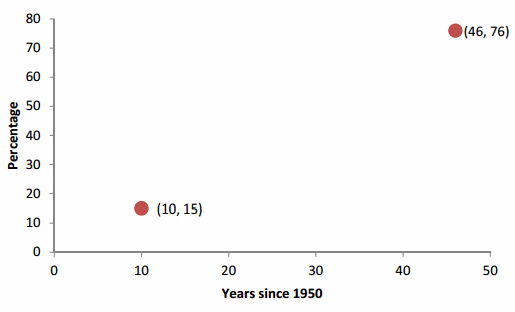
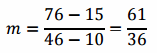
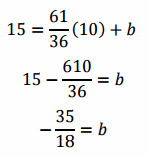
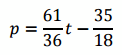
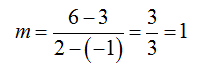
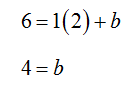
 In
In