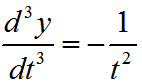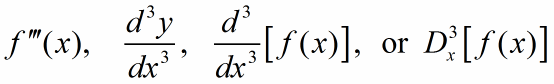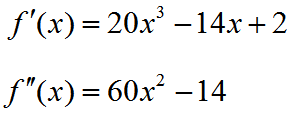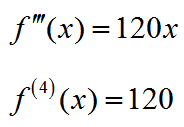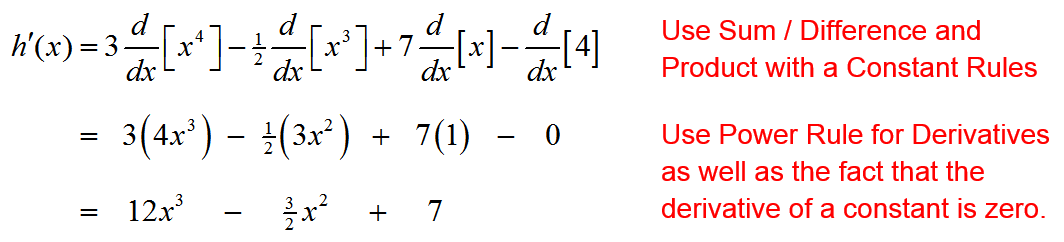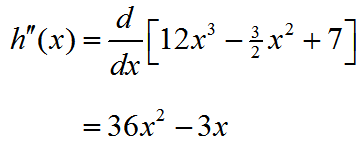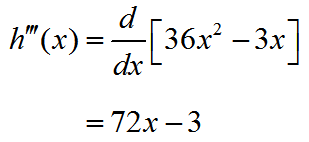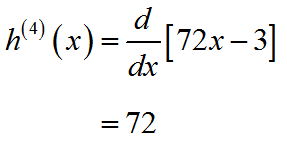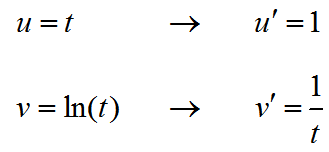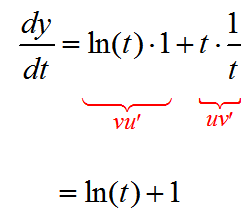How are other higher derivatives calculated?
The second derivative is an example of a higher derivative. By taking the derivative of the second derivative, we obtain another higher derivative, the third derivative. The notation for the third derivative follows the pattern established by the second derivative.
Any of the following notations may be used to write the third derivative of a function y = f (x):
By taking the derivative of another derivative, we may calculate other higher derivatives. These higher derivatives may be written in a similar manner. For derivatives higher than the third derivative, we write the nth derivative as f (n)(x).
For the function f (x) = 5x4 – 7x2 + 2x – 1, the first and second derivatives were calculated earlier as
The derivative of the second derivative, the third derivative, is calculated by taking the derivative of the second derivative. We can continue to take the derivative of the derivative to obtain higher derivatives:
Since the derivative of a constant is zero, the fifth derivative and those higher are equal to zero.
Example 4 Calculate the Fourth Derivative
Let
Find the fourth derivative h(4) (x).
Solution The first derivative is
We can follow the same strategy to get the second derivative,
the third derivative,
and the fourth derivative,
Example 5 Calculate the Third Derivative
Let
Find the third derivative 
Solution To find the first derivative, use the Product Rule for Derivatives with the factors and corresponding derivatives,
The product rule leads to
The second derivative is simply the derivative of the first derivative or
Rewrite 
as t -1 to make the next derivative easy to do. The third derivative is
The third derivative is rewritten with a positive exponent as 
.