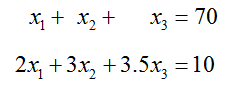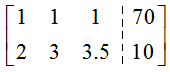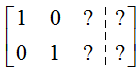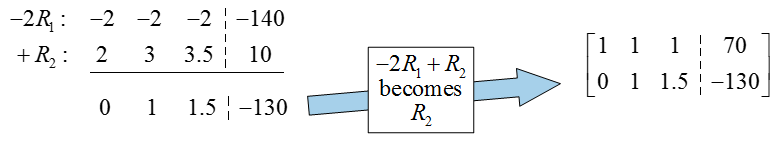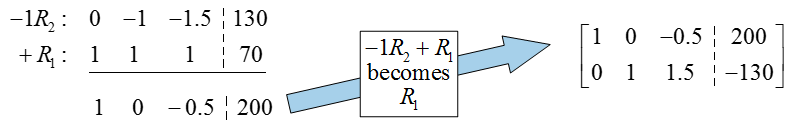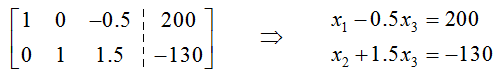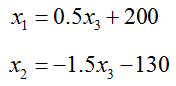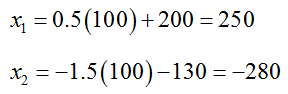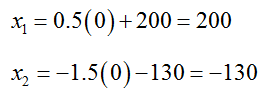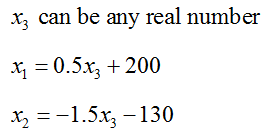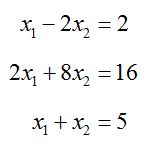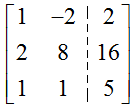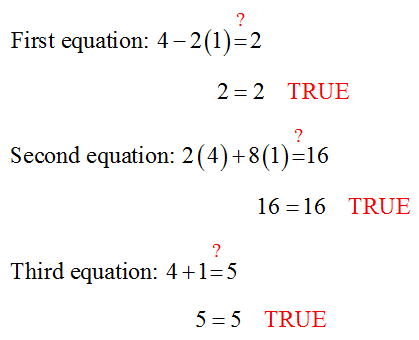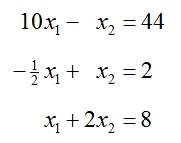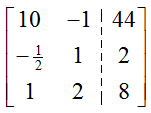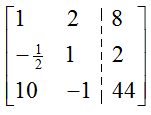Do all systems of linear equations have unique solutions?
Earlier we examined two systems where the numbers of variables was equal to the number of equations. Often there are fewer equations than variables or more equations than variables. Even in systems where the number of variables initially equals the number of equations, one of the rows may become all zeros, meaning that the equation was unnecessary. In all of these cases, we can still use the strategy from Question 3 to solve the problem.
Example 6 Solve a System with More Variables Than Equations
Solve the system of equations
by transforming its augmented matrix to reduced row echelon form.
Solution This system does not use x, y, and z like earlier examples. However, if we let the first column in the augmented matrix correspond to x1, the second column to x2, and the third column to x3, we can write the augmented matrix for this system as
To put this matrix into reduced row echelon form, we must transform it using row operations to
Since there is no third row, we have no hope of solving for a solution where x1, x2, and x3 are each a unique value. Instead, we’ll be able to solve for x1 and x2 in terms of x3.
The original augmented matrix already has a 1 in the first column and row, so there is no need to put a pivot there. To put a 0 below the pivot, multiply the first row by -2, add it to the second row, and put the result in place of the second row:
The previous row operation not only put a 0 in the first column, but also placed the pivot in the second row and column (very lucky!). To put this matrix into reduced row echelon form, we need to put a zero above the pivot in the second column. Multiply the second row by -1, add it to the first row, and place the result in the first row:
This matrix is in reduced row echelon form, but we can’t read the solution off as we have in earlier examples. If we convert this back to a system of equations, we get
Notice that each of these equations contains x3 and it is easy to solve for x1 in the first equation and x2 in the second equation. If we solve for x1 and x2 we get
Although we don’t have specific numbers for each variable, we do have a recipe for finding values. If we choose any value for x3, we can find the corresponding values for x1 and x2. For instance, if we choose x3 = 100, then
If x3 = 0, then
Since x3 can be any number, there are an infinite number of solutions to the system. However, not just any combination of numbers works. Once a value for x3 is chosen, the equations above must be used to calculate corresponding values for x1 and x2. This can be summarized by writing
In this case, we have more variables than equations so we would expect to be able to solve for only some of the variables explicitly. In each row we can solve for a variable explicitly as long as the row is not entirely zeros. Any variables beyond the number of nonzero rows, in this case one, will be values that we can pick. These variables are called parameters. Parameters are variables whose values are arbitrary and can be picked to be anything that is reasonable for the system of equations.
Example 7 Solve a System with More Equations Than Variables
Solve the system of equations
by transforming its augmented matrix to reduced row echelon form.
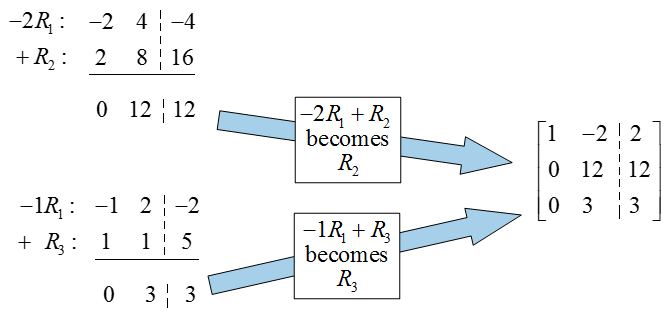
Solution The augmented matrix for this system is
To put this matrix into reduced row echelon form, we need to place pivots in the first and second columns and zeros in the rest of these columns.
The entry in the first column and row is a 1 so the pivot is already in place. To put zeros below the pivot,
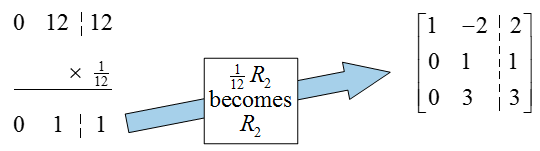
In the second column and row, we need to transform the 12 to a 1 by multiplying the row by 1/12:
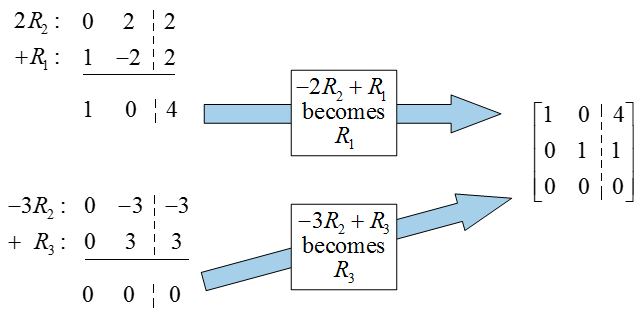
Now place zeros in the rest of the column,
If we convert this matrix back to a system of equations, we find that x1 = 4 and x2 = 1. Notice that the last row of the matrix is all zeros and does not contribute to the solution. This means that there are two variables and two nonzero rows so no parameters are needed in the solution.
We can check the solution by substituting (4, 1) into each equation:
Since (x1, x2) = (4, 1) satisfies each equation in the system, it is the solution to the original system of equations.
Example 8 Solve a System with More Equations Than Variables
Solve
by transforming its augmented matrix to reduced row echelon form.
Solution Like the last example, we’ll let the first column in the augmented matrix correspond to and the second column to . The augmented matrix for this system is
To create a pivot in the first row and column, we have two possibilities. We could multiply the first row by 1/10 or interchange the first and third row. Since interchanging rows does not introduce and fractions into the matrix, we’ll do that to yield
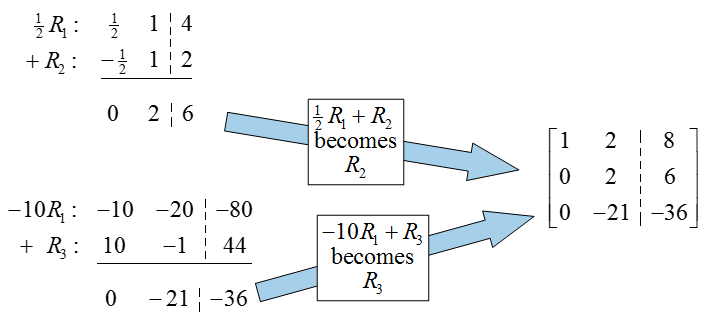
Now we’ll use row operations to fill the rest of the first column with zeros:
To create a pivot in the second row and column, multiply the second row by 1/2:
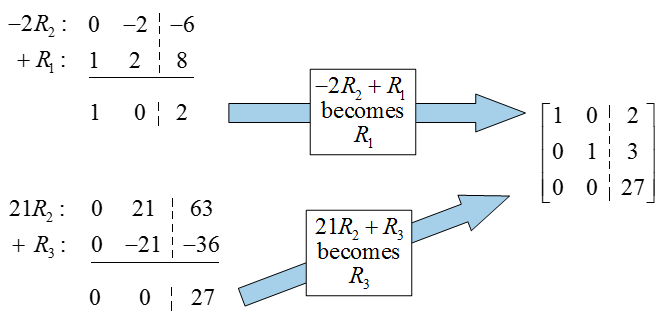
Now use row operations to place zeros above and below the pivot in the second column:
The first two rows in the reduced row echelon form suggest a solution, but the third is problematic. If we write this row as an equation, we get
The left side is simply 0. Since 0 cannot equal 27, this implies that there are no solutions to this system. This system is an inconsistent system.
These examples illustrate what may happen when there are more equations than variables or when there are more variables than equations. It is possible for the system to have a unique solution as in Example 5. The system may be a system with infinitely many solutions like Example 6 or have no solutions like the inconsistent system in Example 8.