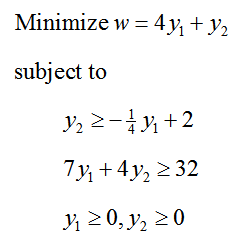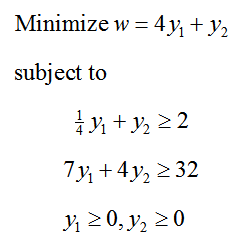Section 4.4 Question 1

What is a standard minimization problem?

In Section 4.3, we learned that some types of linear programming problems, where the objective function is maximized, are called standard maximization problems. A similar form exists for another for linear programming problems where the objective function is minimized.

A standard minimization problem is a type of linear programming problem in which the objective function is to be minimized and has the form

w = d₁ y₁ + d₂ y₂ + … + d_n y_n

where d₁, … , d_n are real numbers and y₁, … , y_n are decision variables. The decision variables must represent non-negative values. The other constraints for the standard minimization problem have the form

e₁ y₁ + e₂ y₂ + … + e_n y_n≥ f

where e₁, … , e_n and f are real numbers and f ≥ 0.

The standard minimization problem is written with the decision variables y₁, … , y_n, but any letters could be used as long as the standard minimization problem and the corresponding dual maximization problem do not share the same variable names.

Often a problem can be rewritten to put it into standard minimization form. In particular, constraints are often manipulated algebraically so the each constraint has the form e₁ y₁ + e₂ y₂ + … + e_n y_n≥ f. Example 1 demonstrates how a constraint can be changed to put it in the proper form.

For the problems in this section, we will require the coefficients of the objective function be positive. Although this is not a requirement of the Simplex Method, it simplifies the presentation in this section.

Example 1 Write As A Standard Minimization Problem

In Section 4.2, we solved the linear programming problem

using a graph. Rewrite this linear programming problem as a standard minimization problem.

Solution In a standard minimization problem, the objective function must have the form w = d₁ y₁ + d₂ y₂ + … + d_n y_nwhere d₁, … , d_n are real number constants and y₁, … , y_nare the decision variables. The objective function matches this form with .

Each constraint must have the form e₁ y₁ + e₂ y₂ + … + e_n y_n≥ f where e₁, … , e_n and f are real number constants. Additionally, the constant f must be non-negative. The second constraint, 7y₁ + 4y₂ ≥ 32, fits this form perfectly.

The first constraint appears to have the correct type of terms, but variable terms are on both sides of the inequality. To put in the proper format, add ¹/₄y₁ to both sides of the inequality:

¹/₄ y₁ + y₂ ≥ 2

With this change, we can write the problem as a standard minimization problem,

In addition to adding and subtracting terms to a constraint, we can also multiply or divide the terms in a constraint by nonzero real numbers. However, remember that the direction of the inequality changes when you multiply or divide by a negative number. This can complicate or even prevent a linear programming problem from being changed to standard minimization form.