y = Pert
This allows us to incorporate exponential function into the College Algebra curriculum as well as logarithms.
The project letter for this project is very similar to earlier project letters in the series.
- College Costs (Exponential) Project Letter (PDF)
The goal of this project is to find the savings using exponential models for two-year and four-year college costs. These models will pass through two of the data points for each dataset. Students complete one technology assignment to help them find the model.
- Technology Assignment – Find an Exponential Function for College Costs (PDF)
For the US two-year college data at (6, 2018) and (9, 2285), we substitute the values into the model to obtain the nonlinear system, 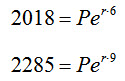
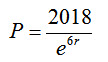
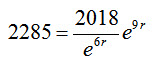
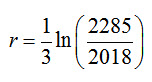
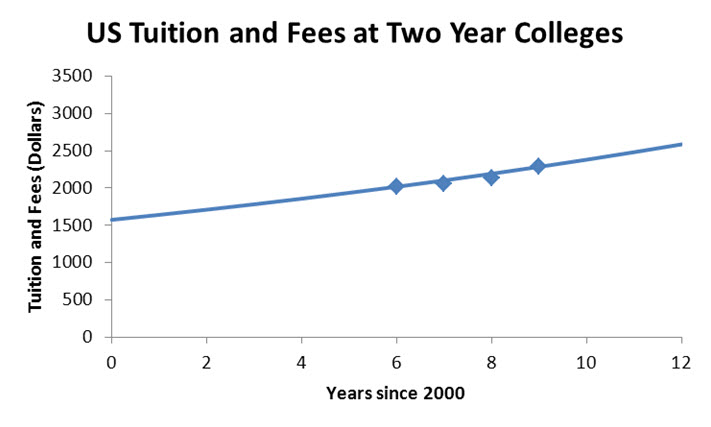
Savings = F(13) + F(14) – T(13) – T(14)
over the period 2013-2017.
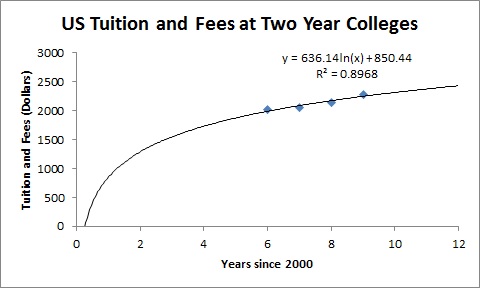
The fourth project functions as a final in my College Algebra class. As with the earlier project, it focuses on the savings accrued from attending two-year college to earn a four-year degree. In this project, students find a logarithmic regression model of the form
y = a + b ln(x)
Since this takes the place of a final exam, each student is on their own to find the model. No technology assignments are assigned. Using some type of technology, students produce a logarithmic function like the one below and use it to calculate the savings.
This series of projects exposes students to thee key concepts in college algebra repeatedly. This repeated retrieval helps them to learn exactly what a model is and how it might be used. The projects are far from easy and have many possible tangents that students may focus on. This effort forces them to really understand what they are doing.