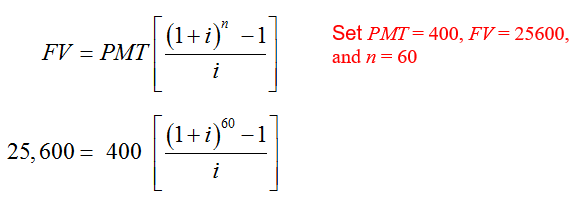Category: College Math

How Do I Find The Payment On A Loan That Is Amortized?

A couple of you have had trouble finding the payment properly. I am not sure whether this is a calculator issue (there is a screen capture for the payment in Question 3 of Section 5.4) or a formula issue. Often I see people using the interest rate for i instead of the interest rate per period. Remember, since i is the interest rate per period you need to divide it by the number of periods in a year.

Here is an additional example of finding the payment and then using it to construct an amortization table.

How Do I Find The Rate For A Sinking Fund?

To find the rate for a sinking fund, you needed to use a graph or the TVM Solver on a TI graphing calculator to find the interest rate on a sinking fund. Let’s look at the most basic way of doing this by graphing.

Problem Find the interest rate needed for a sinking fund to accumulate 25,600 dollars in five years with monthly payments (made at the end of the month) of 400 dollars.

Solution Since this problem indicates that payments are being made, we need to use the ordinary annuity formula. For a sinking fund, the future value is known, 25600. We also know the payment, 400, and the number of periods, 60:

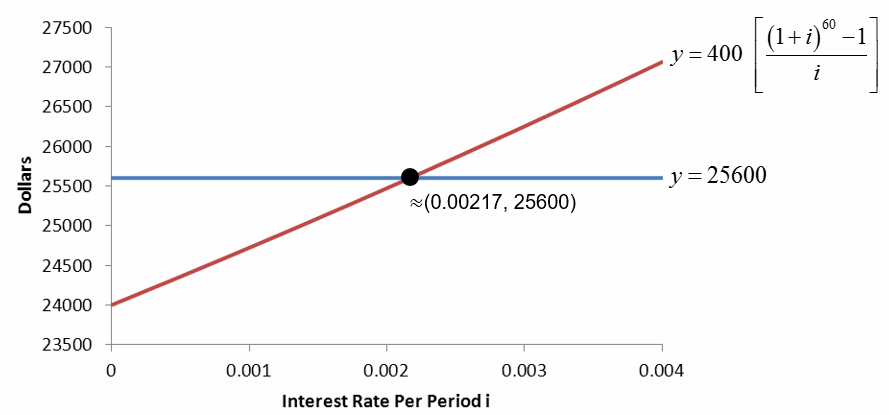
This is incredibly difficult to solve for i algebraically. Instead, graph each side of the equation and look for a point of intersection. On a graphing calculator we would type y1 = 400*((1+x)^60-1)/x and y2 = 25600 in the window [0, 0.004] by [23500, 27500].

The toughest part is coming up with the window on the graph. Since the x on your calculator represents the interest rate per period, it needs to small like 0 to 0.01 initially. The vertical window is much easier to determine since the second equation is y = 25600, a horizontal line. Simply pick a horizontal window that spans this value.

The annual interest rate is 12 · 0.00217 ≈ 0.02604 or approximately 2.6%.

How Do I Deal With Variables Other Than x in Linear Functions?

When working with functions with unusual variable names and scaling, students often run into two problems.

  • trouble with what each variable represents
  • trouble with the scaling of the variables

Since we rarely use x in Finite Math to represent the independent variable, we need to get used to these names. Typically, the variables are aligned or scaled. This means we need to pay particular care to interpreting answers.

In one type of the problem, you are given a demand function $latex \displaystyle p=D(q)=32-1.25q$ where p is the price in dollars and q is the quantity of watches demanded in hundreds. In part b, you were asked to find the price when the demand is 800 watches. This quantity corresponds to $latex \displaystyle q=8$ and gives a price of

$latex \displaystyle D(8)=32-1.25(8)=22$

Notice how the scaling on the variable works…800 watches is input as 8 hundred. In part c, you need to find the demand when the price is 27 dollars. Now we know the output from the function and we need to find the corresponding input,

$latex \displaystyle 32-1.25q=27$

When we solve this for q we get $latex \displaystyle q=4$. In other words, 4 hundred watches are demanded when the price is 27 dollars. Since the units on the answer blank is watches, you will need to type 400 in the answer blank. I think many of you were not taking the units into account on this problem. Units are incredibly important in the real world where you are dealing with millions of dollars. In those cases misinterpreting 2,000,000 dollars and 2 million dollars may cost you your job.