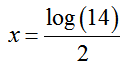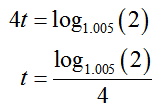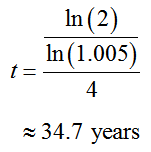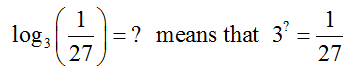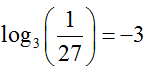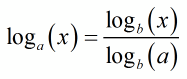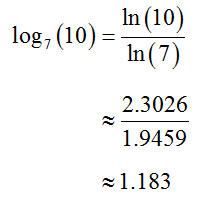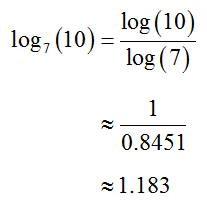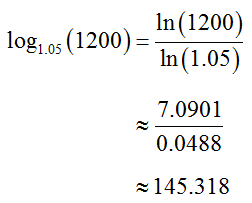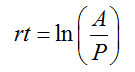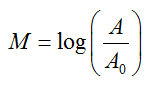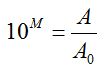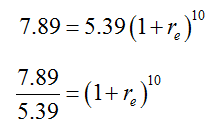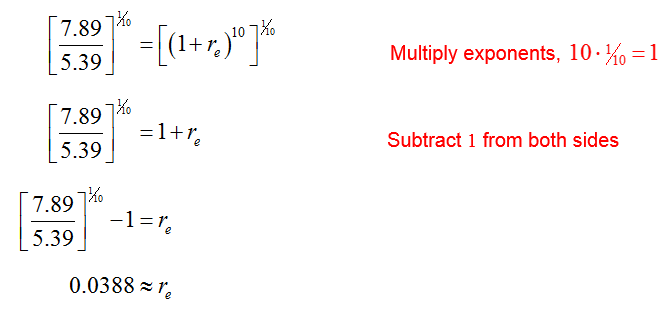Category: Finite Mathematics Ebook

How do you solve problems involving using logarithms?

Logarithms are useful for solving exponential equations. An example of an exponential equation is the equation

To solve this equation for the variable x, isolate the term containing the exponential piece. This is done by subtracting 2 from both sides of the equation to give

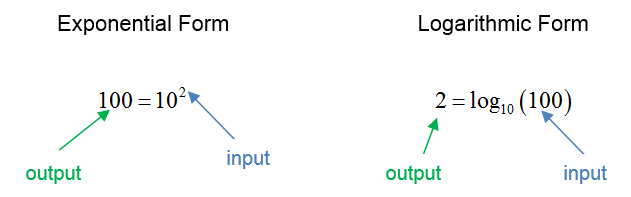
We remove the variable from the exponent by converting this exponential form to logarithmic form. The logarithmic form is

Divide both sides of the equation by 2 to yield

This is the exact solution to the original exponential equation. We can use this expression to find an approximate solution to as many decimal places as needed. To three decimal, the solution is x ≈ 0.573. If we had worked out the logarithm earlier in the calculation, we would not be able to write down the exact solution. The best practice is to find the exact solution first. Use the exact solution to get an approximate solution.

Example 6         Compound Interest

How long will it take$10,000 to double in an account earning 2% compounded quarterly?

Solution For this problem, we’ll use the Compound Interest Formula

Since we want to know how long it will take, let t represent the time in years. The number of compounding periods is four times the time or n = 4t.  The original amount is PV = 10,000 and the future value is double or FV = 20,000. The interest rate per period is . When these values are substituted into the compound interest formula, we get the exponential equation

To solve this equation for t, isolate the exponential factor by dividing both sides by 10,000 to give

Convert this exponential form to logarithm form and divide by 4,

To find an approximate value, use the Change of Base Formula to convert to a natural logarithm (or a common logarithm):

It is interesting to note that the starting amount is irrelevant when doubling. If we started with P dollars and wanted to accumulate 2P at the same interests rate and compounding periods, we would need to solve

This reduces to the same equation as above,

when both sides are divided by P. This means it takes about 37.4 years to double any amount of money at an interest rate of 2% compounded quarterly.

---

In this example, converting to logarithm form removes the variable from the power in the exponential factor. This makes it easy to solve for the variable. This same strategy is used to solve for other variables in the power of an exponential also.

Example 7         Continuous Exponential Decay

The value of a large piece of equipment depreciates from $125,000 to $50,000 in five years. If the value decreases exponentially, at what continuous rate is the value dropping?

Solution We will model the value V of the equipment at some time t years later with the equation

In this equation, the original value of the equipment is V0. The value is decreasing at a continuous rate of r  (as a percent) due to the negative sign in the power. Put the values in this equation to yield

Solve for the rate r by converting to logarithmic form:

This is the exact rate which may be evaluated and rounded to three decimal places to give r ≈ 0.183. The equipment is depreciating at a continuous rate of approximately 18.3 percent per year.

---

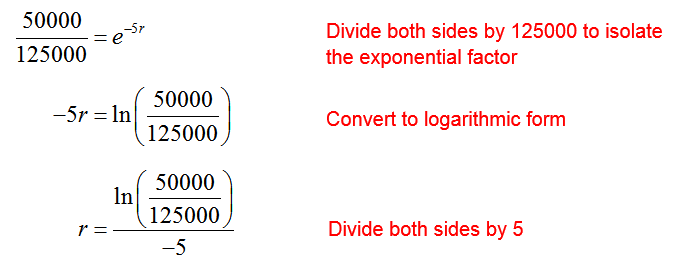
Note that the rate is always given as a percent per some time period. This time period is the same as the units on the variable t.

How do you evaluate a logarithm?

Many logarithms may be calculated by converting them to exponential form. Suppose we want to calculate the value of log₂(16). Start by writing this expression as a logarithmic form,

 We could write the output with a variable, but a question mark suffices to indicate what we want to find. If we convert this form to an exponential form with a base of 2,

The left hand side may be written with the base 2 as 2⁴. Substitute this expression in place of 16,

Since the exponent on the left side must be 4, this is also the value in the original exponential form,

This strategy works well as long as we can write the number on the right with the same base as the exponential on the other side of the equation.

Example 4         Evaluate the Logarithm

Find the value of each logarithm by converting to exponential form.

a.  

Solution Write the logarithm in logarithmic form and convert to exponential form,

Since the value of the logarithm is 2,

b.   

Solution The logarithmic and exponential forms are

Since  the value of the logarithm is -3, The negative power makes the reciprocal.

c.   

Solution The logarithmic and exponential forms are

The value of the logarithm is 2, In effect, the number 2 is put into the base of e and the natural logarithm reverses this process.

---

Not every logarithm may be solved by converting to exponential form. For this strategy to work, we must be able to write each side of the exponential form with the same base.

Scientific and graphing calculators are both able to calculate natural logarithms and common logarithms. Natural logarithms are calculated using a button labeled something like LN. Using this button, you should be able to do the following calculations by pressing the LN button, entering the number, and pressing the ENTER or = button.

You may also calculate common logarithms in a similar manner using a button that is typically labeled LOG. Using this button, you should be able to compute each of the following common logarithms.

Using these buttons, you can compute any natural or common log. Even the logs that may not be solved by converting to exponential form may be computed on a calculator. Some calculator may even have a button for calculating a logarithm with any positive base. To see if your calculator is able to do this, consult the manual for your calculator. If your calculator does not have this button, you can use the change of base formula to compute logarithms with any positive base.

This formula is used to compute a logarithm with base a by converting it to two logarithms with base b. The base b can be any positive number not equal to 1, but usually it is a base of 10 or e so that a calculator may be used to compute the right hand side of the formula.

Example 5         Compute the Logarithm

Find the value of each logarithm using the Change of Base formula for Logarithms.

a.  

Solution We may use the Change of Base formula to convert this logarithm to natural logarithms or common logarithms. If we convert to natural logarithms we get

A calculator is used to evaluate the natural logarithms. The values of the individual logarithms are shown above, but it is a good  idea to type the entire expression. This avoids rounding in the middle of the problem and then rounding again at the end. Ideally you should only round once.

If we convert to common logarithms,

The value of the original base 7 logarithm is the same whether it is computed from natural logs or common logs.

b.  

Solution Use the Change of Base formula with natural logarithms to give

You may also calculate the value using common logarithms,

What is continuous compound interest?

As the frequency of compounding increases, the effective interest rate also increases. We can see this by computing the effective interest rate at a specific nominal rate, say r = 0.1.

As the number of conversion periods per year increases, the effective interest rate gets closer and closer to 0.105171.

In fact, it is possible to show that the effective interest rate gets closer and closer to the value e^0.1 – 1 as the frequency of computing increases. If this is done at a nominal rate of r = 0.1, the accumulated amount is

In general, as the frequency of compounding increases, the effective interest rate gets closer and closer to e^r – 1. We can express this symbolically by writing,

Think of the symbol → as meaning “approaches”.

Larger and larger values of m mean that we are compounding interest more and more frequently. When this happens, we say that the interest is term compounded continuously.

Like the compound interest formula, this formula may also be written in several equivalent forms. In a biological context, the size of a population P with an initial amount of P₀ growing at a continuous rate of r % per year over t years grows according to

In some business applications, an original amount of money or principal P grows to an accumulated amount A at a continuous rate of r % per year over t years according to

In each of these applications, some quantity is growing at a continuous rate r. The original amount of the quantity is multiplied by a factor of e^rt to yield the amount of the quantity at some later time.

Example 7         Continuous Interest

Third Federal Savings and Loan offers a CD that earns 1.79% compounded quarterly (on February 3, 2012). If $5000 is invested in the CD, how much more money would be in the account in 5 years if the interest is compounded continuously versus quarterly?

Solution The future value with interest compounded quarterly is

The future value with interest compounded continuously is

The future value with continuous interest is greater than the future value with interest compounded quarterly by

---

In general, compounding some amount continuously will always yield a larger amount than compounding the same amount at the same rate a finite number of times per year. The greater number of times the amount is compounded in a year, the closer the future value will be to the future value compounded continuously.

How do you convert between the exponential and logarithmic forms of an equation?

Exponential and logarithm functions are inverses of each other. In the simple terms, this means that an expression in exponential form may be converted to logarithm form by switching the inputs and outputs. Let’s start with a concrete example. The exponential function

takes the variable x as its input and outputs the variable y. For an input of x = 2 we get an output of y = 100 since

On a logarithm of base 10 (called a common logarithm), these roles are reversed. The common logarithm must take in y = 100 and output x = 2,

 For common logarithms, those with base 10, the base on the logarithm is often left out and written as

This means that whenever you see a logarithm without a base, it is assumed to have a base of 10. Let’s compare these forms side by side.

The base on the exponential form is below the 2. On the logarithm form, the base is just after and slightly below the word log. The exponential form take in 2 and outputs 100. The logarithm form does exactly the opposite. It takes in 100 and outputs 2. The numbers are the same, but they role they play is reversed.

Example 1      Convert to Logarithmic Form

Convert each exponential form below to its equivalent logarithmic form.

a.   

Solution For this exponential form, the base is 10 so it will convert to a logarithm base 10 or common logarithm.  The input is 3 and the output is 1000. When this exponential is converted to a logarithm, the input will be 1000 and the output will be 3. This gives the logarithmic form,

Note that the original exponential form has the exponent on the left side instead of the right. Where it appears is irrelevant. They key is to recognize that the exponent is the input and the other side of the form is the output.

b.   

Solution This exponential form will convert to a logarithm with a base of 2. Since the input is 5 and the output is 32, the logarithmic form is

c.   

Solution Even though the input and output have  variables, we may still reverse the roles and write logarithmic form as

---

The base e occurs frequently in business and finance. Like the constant π, the constant e  represents an irrational number whose value is approximately 2.718. Because this is an approximation, you’ll often see the approximately equal sign, ≈, when using this base. Most scientific and graphing calculators have an e button to help you evaluate exponentials with a base of e.

Exponential forms with a base of e convert to logarithms with a base of e. For instance,

Logarithms with a base of e are also called natural logarithms. They are often abbreviated by writing  2 ≈ ln(7.389) instead of  2 ≈ log_e(7.389).

Example 2         Convert to Logarithmic Form

Convert each exponential form with a base of e to logarithmic form.

a.  e⁰ = 1

Solution The logarithmic form for this exponential form is

ln(1) = 0

b.  

Solution In this exponential form, groups of variables play the role of input and output. The input in the exponential form is  and the output is the fraction The corresponding natural logarithm is

---

Logarithmic forms may also be converted to exponential form. As with exponential form, they key is to identify the input and output and switch those roles.

Example 3         Convert to Exponential Form

Convert each logarithmic form to exponential form.

a.   

Solution This form converts to an exponential form with a base of 4. The input on the logarithmic form is 64 and the output is 3. The corresponding exponential form is

b.  

Solution Before identifying the input and output, isolate the logarithm. This is done by subtracting b from both sides to yield

In this form, the input to the logarithm is x and the output is y – b. The exponential form is

c.   

Solution The input on this common logarithm is the group  and the output is M. Switching these roles gives the exponential form

What is an effective interest rate?

The amount of interest compounded depends on several factors. The nominal rate r and the number of conversion periods m both influence the future value over a predetermined time period. A savings account earning a higher nominal rate over fewer conversion periods might have the same future value as another savings account with a lower nominal rate and a higher number of conversion periods. To help us compare nominal interest rates, we use the effective interest rate. The effective interest rate is the annual interest rate that leads to the same future value in one year as the nominal interest rate compounded m times per year.

Another name for the effective interest rate is the effective annual rate or annual percent yield (APY).

Example 5         Best Investment

An investor has the opportunity to invest in one of two opportunities. The first opportunity is a certificate of deposit (CD) earning 1.140% compounded daily. The second opportunity is an investment yielding a dividend of 1.141% compounded quarterly. Which investment is best?

Solution The better investment is the one with the higher effective interest rate. The nominal rate for the CD is r = 0.01140. Interest is earned on a daily basis so m = 365. This gives an effective rate of

For the other investment, r = 0.01141 and m = 4. The effective rate for this investment is

The effective rate for the CD, 1.1147%, is higher than the effective rate for the investment, 1.1146%. Because of this, the CD is the better investment.

---

By law, the effective rate of interest is shown in all transactions involving interest charges. The APY is always prevalent in advertisements, such as the one below for five-year CD rates from Bankrate.com on December 29, 2011.

We can also use the APY to compute accumulated amounts. Suppose we want to compute the future value from depositing $1000 in the Bank of America five year CD. We could calculate the future value using the rate,

Alternatively, we compute the future value using the APY and compound annually,

This gives us another way of computing accumulated amounts.

Since the APY is always shown in financial transactions, this formula allows us to compute accumulated amounts from the APY.

We can also use the compound interest formula to find the rate at which an amount grows. In this case, we think of PV as the original amount and FV as the amount it grows to.

Example 6      Growth of Ticket Prices

In 2000, the average price of a movies theater ticket was $5.39. In 2010, the average price increased to $7.89. At what effective percentage rate did prices increase over the period from 2000 to 2010 on average?

Source: National Association of Theater Owners

Solution The original price in 2000 is $ 5.39. This price grows in ten years to $7.89. Use these values in to find the effective rate :

To solve for , remove the tenth power by raising both sides of the equation to the one-tenth power.

Over this period, the price of tickets increased by an average of 3.88% per year.