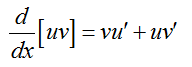Integration by Parts

In section 11.5, you learned how to take the derivative of a product. For a product of two function of the variable x, called u and v, the derivative of the product is

In this form, the variable on each function has been left off to make the rule easier to remember.

In this section, we’ll learn how to reverse the product rule. This technique is called integration by parts. It helps you to find the antiderivative of functions that are written as a product.

Read in Section 14.2

• How do we find the antiderivative of functions involving products?
• How is the exact area under a function involving products computed?

Section 14.2 Workbook (PDF) – 9/5/19

Watch Videos

Do Homework for Section 14.2