Last week I wrote about using relevant examples in Relevance and Meaning Before Details. In this post, I suggested that the meaning of concepts need to be presented before the details. This sounds like a great idea, however I have to admit that I am as guilty as the next instructor when it comes to skipping the meaning in the face of huge amounts of content.
Logarithms are a topic in College Algebra that strikes fear into many students hearts. Most students have had a little exposure to them…not a pleasurable experience. This semester I was determined to introduce logarithms with an example…even at the expense of a few theoretical examples. At this point in the semester, the interest of the students is waning. Attendance is down. I needed to them to understand why logarithms exist.
I started the class with an excerpt from a video on the Japanese earthquake in 2011. This is the point in the class where their attention is highest and I wanted to take advantage of this.
I had trouble getting the audio to play since the speakers on the computer had been muted. Once I took care of that minor issue, the video played for several minutes. After a while several students commented on their own experience with earthquakes. With this buy-in, I went through this brief introduction to the Richter scale. For non-mathematicians, don’t despair…
Seismologists study earthquakes. They measure the intensity I of earthquakes in terms of how much more powerful the quake is than a quake with minimum intensity I0. This is represented by the ratio
$latex \displaystyle \frac{I}{{{I}_{0}}}$
If an earthquake is measured to be 10,000 times the minimum intensity, this ratio is equal to 10,000,
$latex \displaystyle \frac{I}{{{I}_{0}}}=10000$
Because earthquakes can be incredibly intense, this ratio can be very large. The earthquake shown above was 1,000,000,000 times more intense than the minimum intensity. In this case, the ratio is
$latex \displaystyle \frac{I}{{{I}_{0}}}=1,000,000,000$
Seismologists will write the right side as an exponential,
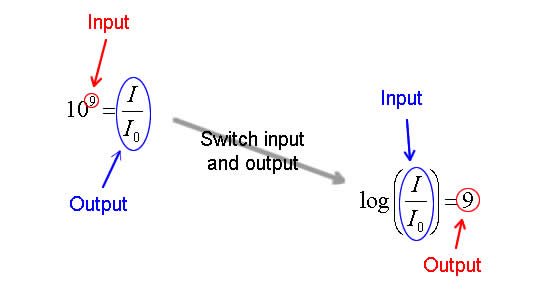
$latex \displaystyle \frac{I}{{{I}_{0}}}={{10}^{9}}$
The power on this exponential, 9, is the Richter rating of the earthquake. Instead of writing down the values of the intensity, scientists think in terms of powers of ten and use the exponent. In the case of the earthquake in Japan in 2011, we would say that the earthquake measured
$latex \displaystyle \text{Richter Magnitude}=9$
Notice that there is no mention of logarithms so far…no need to stoke their fears. I don’t want them thinking about their past troubles when I am trying to deliver meaning. But at some point I need to introduce the idea of the inverse of an exponential function. I did this by graphing a simple exponential function and making the inverse by switching the input and output.
With this background, I touched back on the Richter scale.
Now that I connected with the meaning again (hook!), I worked through a few more examples regarding properties of logarithms.
Another 10 minutes later when their attention is crashing, I related a story of a friend of mine who managed a Costco warehouse in Seattle when a magnitude 5.5 earthquake hit. Let’s just say that pickles, peanut butter, olives and raw sewage was never meant to go together. After this hook, a bit more on logarithm properties to finish the class.
Did I cover as much on this day as I have in past semesters? No. But I think I kept their attention much better…their questions about earthquakes were a testimonial to their attention. Maybe I covered 80% of what I had in previous semesters. But with the higher degree of attention, I think the overall retention of content will be much higher this semester.