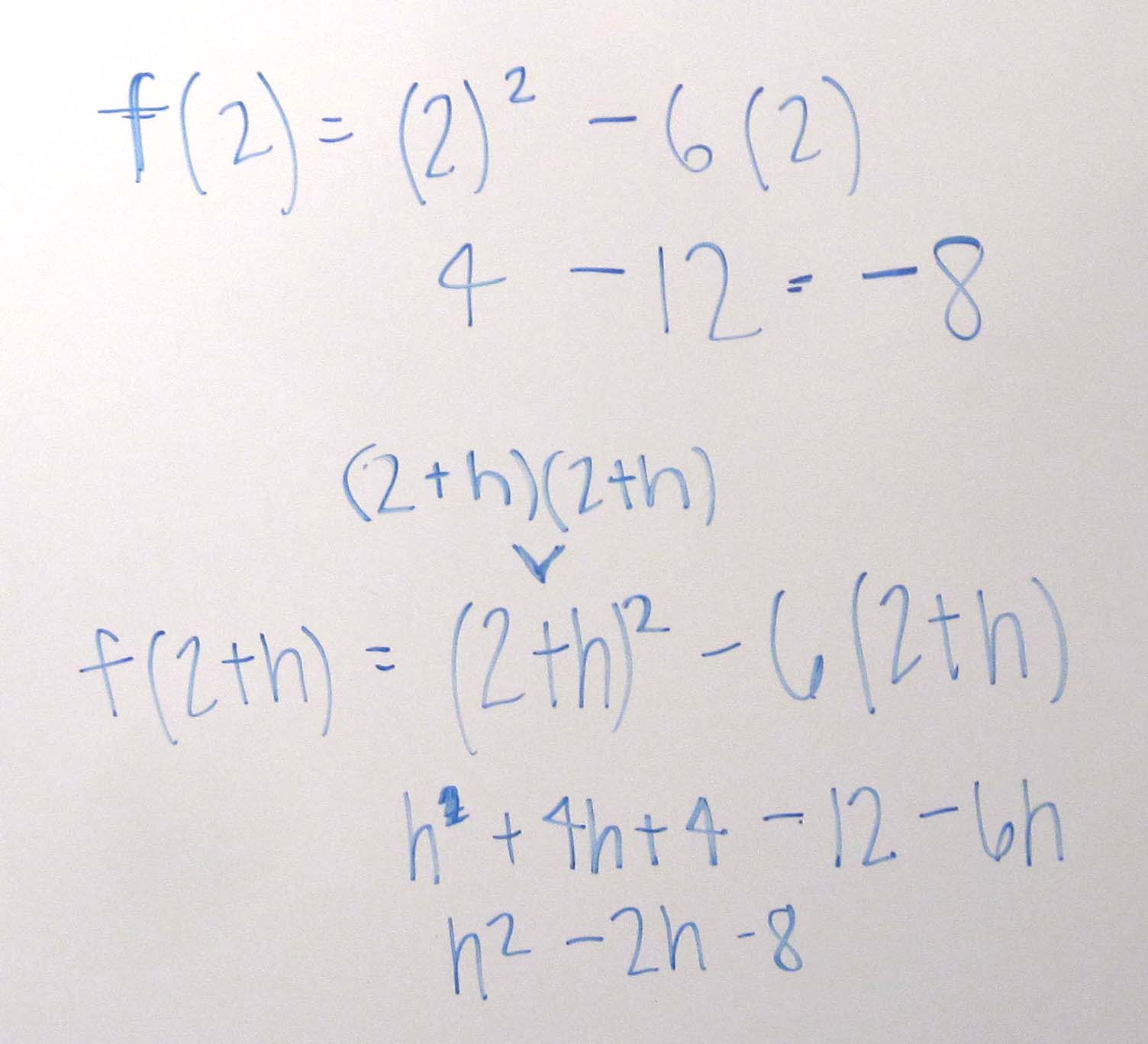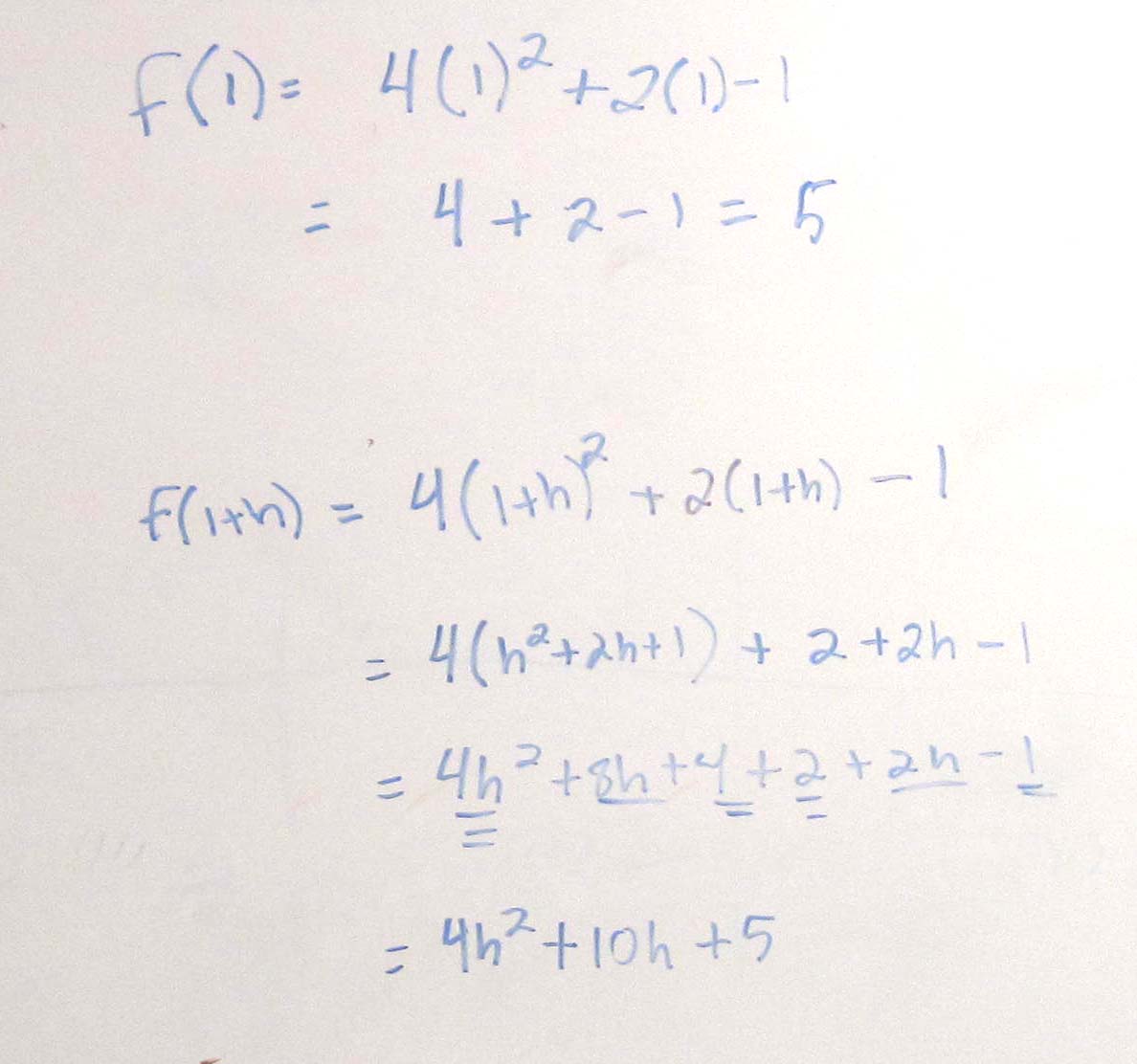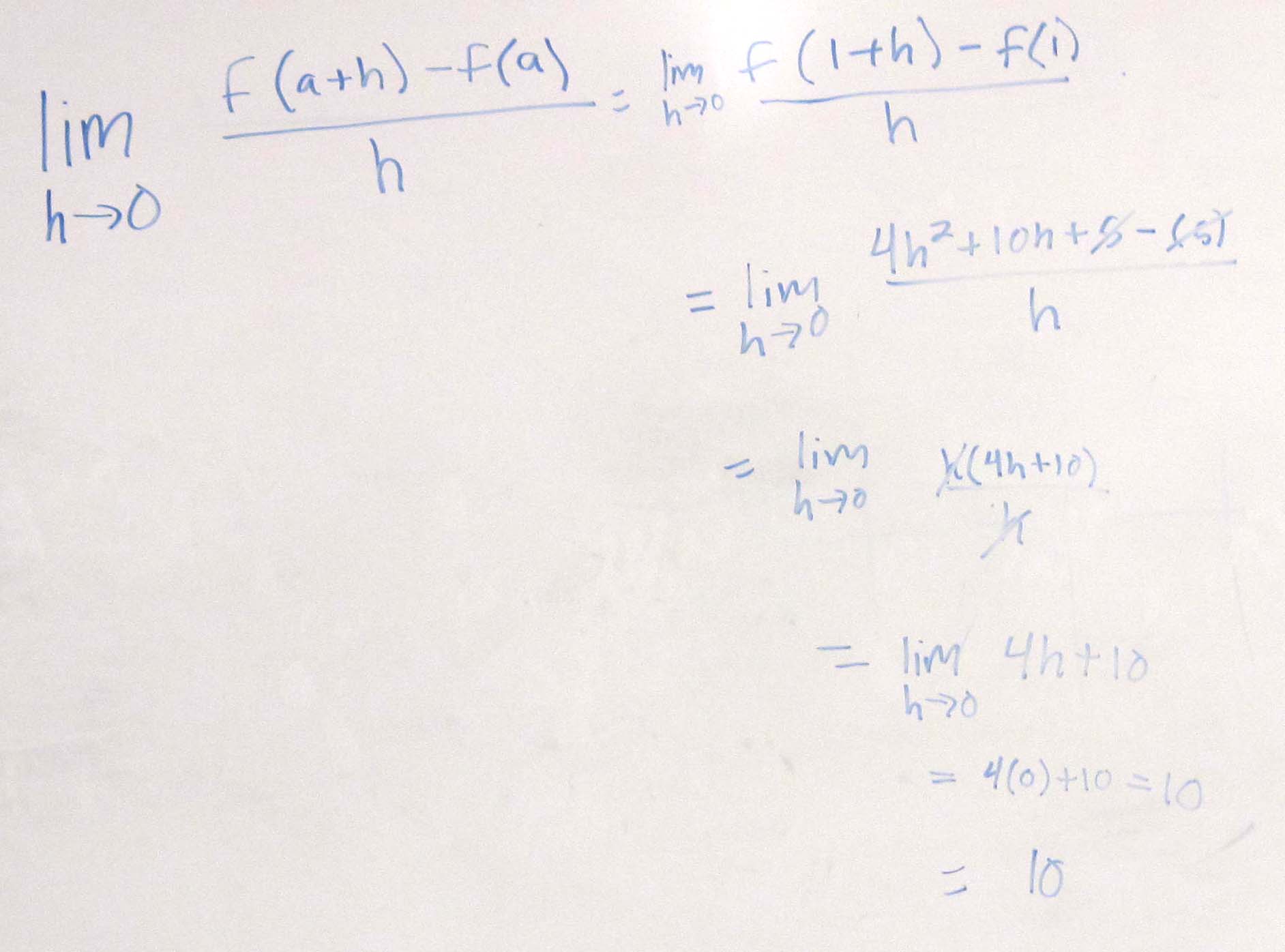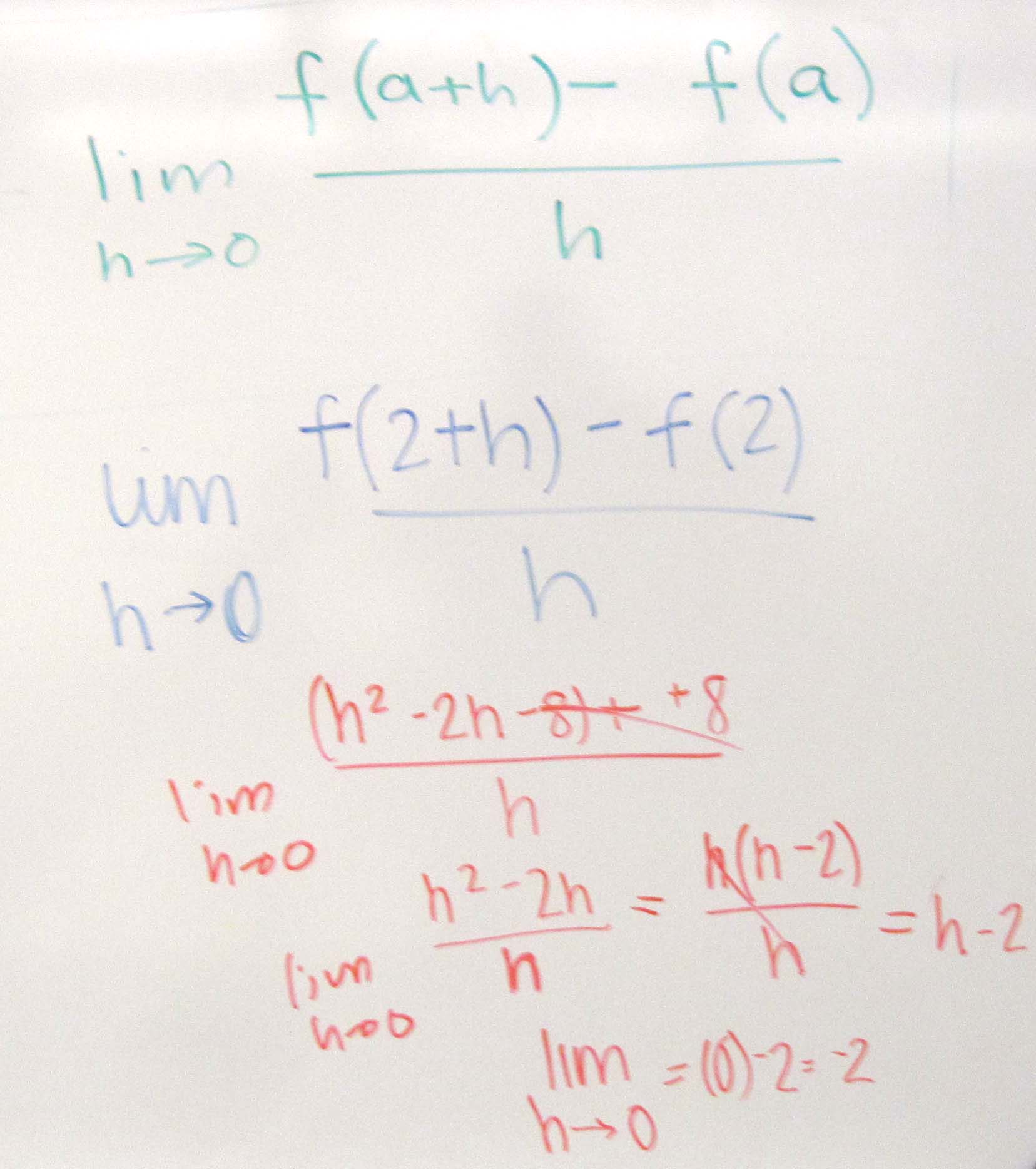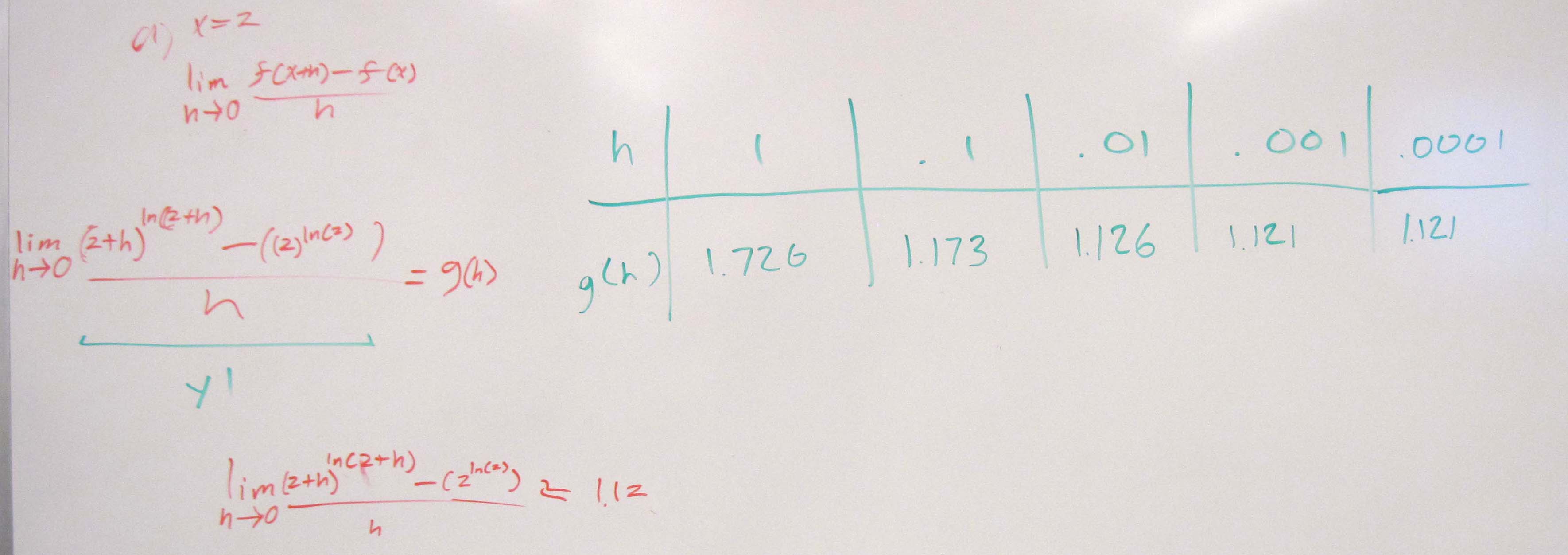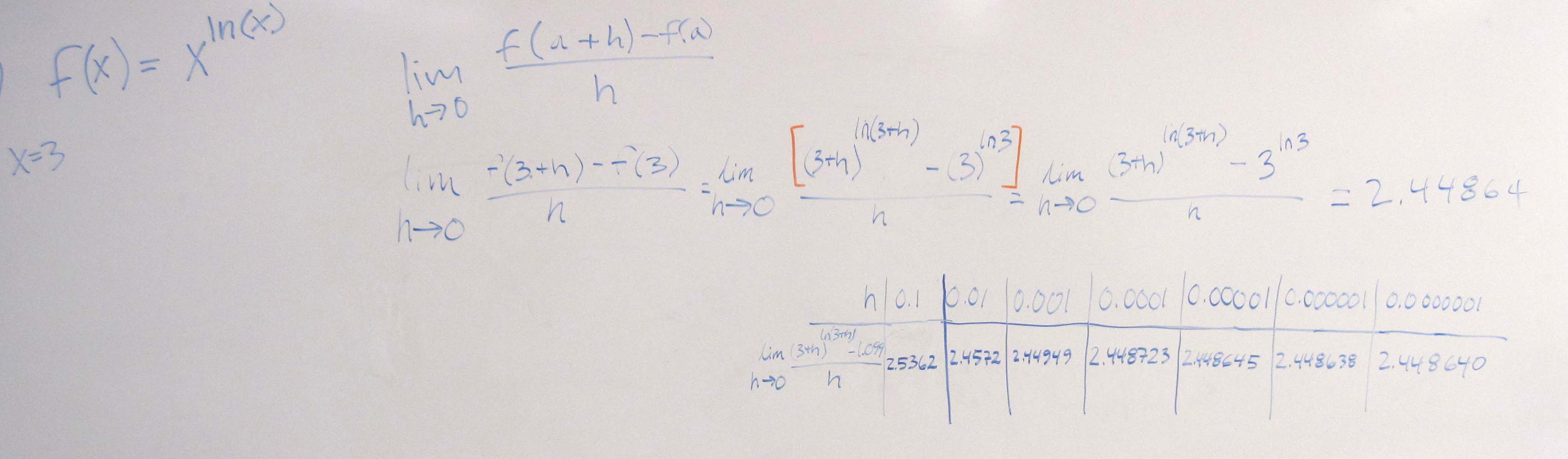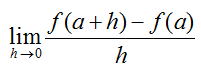Category: Instantaneous Rate of Change

The instantaneous rate of change is calculated to find how fast one quantity changes with respect to another.

The instantaneous rate of change of  f (x)with respect to x at x = a  is

$latex \displaystyle \begin{matrix}
\text{Instantaneous rate of change of }f\text{ } \\
\text{with respect to }x\text{ at }x=a \\
\end{matrix}=\underset{h\,\,\to 0}{\mathop{\lim }}\,\frac{f(a+h)-f(a)}{h}$

To apply this definition, you need to identify the point a at which the rate is to be calculated. Then the function values f (a) and f (a+h) are calculated and simplified. Finally, these are substituted into the limit so that it evaluated.

Example 1 Find the instantaneous rate of change of $latex \displaystyle f(x)=4{{x}^{2}}+2x-1$ at $latex \displaystyle x=1$.

Solution Start by calculating the two function values.

Once you have the function values, substitute them into the definition for instantaneous rate of change.

Example 2 Find the instantaneous rate of change of $latex \displaystyle f(x)={x}^{2}+6x$ at $latex \displaystyle x=2$.

Solution The function values are

Now put these into the limit definition of instantaneous rate of change.

The instantaneous rate of change is calculated using the limit

$latex \displaystyle \begin{matrix}
\text{Instantaneous rate of change of }f\text{ } \\
\text{with respect to }x\text{ at }x=a \\
\end{matrix}=\underset{h\,\,\to 0}{\mathop{\lim }}\,\frac{f(a+h)-f(a)}{h}$

For many functions like polynomials, this limit may be calculated algebraically. When this limit cannot be computed algebraically or is very difficult to compute algebraically, we can use a table to estimate the limit. The problems below illustrate the table for the limit.

Problem 1 Estimate the instantaneous rate of change of f with respect to x at x = 2 if

$latex \displaystyle f(x)={{x}^{\ln (x)}}$

Solution In this problem, a = 2. We need to evaluate

$latex \displaystyle \begin{matrix}
\text{Instantaneous rate of change of }f\text{ } \\
\text{with respect to }x\text{ at }x=2 \\
\end{matrix}=\underset{h\,\,\to 0}{\mathop{\lim }}\,\frac{f(2+h)-f(2)}{h}$

Since the values in the table are shown to three decimal places, we can estimate the rate to two decimal places. In the last two columns, the difference quotient rounds to 1.12 so the rate is approximately 1.12.

Problem 2 Estimate the instantaneous rate of change of f with respect to x at x = 3 if

$latex \displaystyle f(x)={{x}^{\ln (x)}}$

Solution In this problem, a = 3. We need to evaluate

$latex \displaystyle \begin{matrix}
\text{Instantaneous rate of change of }f\text{ } \\
\text{with respect to }x\text{ at }x=3 \\
\end{matrix}=\underset{h\,\,\to 0}{\mathop{\lim }}\,\frac{f(3+h)-f(3)}{h}$

The table shows most values to 6 decimal places. In the last two columns, the values both round to 2.44864.