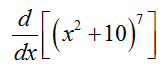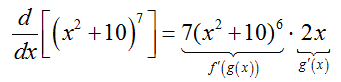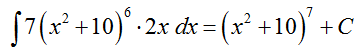The Substitution Method

In Chapter 13, we reversed the derivative process for basic functions like power and exponential functions. By taking the antiderivative of a power function, we were able to find the original function we had taken the derivative of. In this question, we continue to find antiderivatives of function. For example, suppose we want to take the derivative

Since the express is a composition of two functions, we must use the chain rule to take this derivative. Start by identifying the inside and outside functions of the composition,

The derivatives of these functions are

Using the chain rule,

This derivative can also be written as the antiderivative,

If we have already carried out the derivative, writing out the antiderivative is just the reverse process. However, it is rarely the case that we have the derivative available to help us evaluate the antiderivative. For integrands involving compositions, Substitution Method may help us to find the antiderivative.

Read in Section 14.1

• How do we find the antiderivative of functions involving compositions?
• How is the exact area under a function involving compositions computed?
• Handout: Fundamental Theorem Example with Substitution
• Handout: More Examples of Substitution

Section 14.1 Workbook (PDF)– 9/5/19

Watch Video